Page 400 - Mathematical Techniques of Fractional Order Systems

On the Fractional Order Generalized Discrete Maps Chapter | 13 389

TABLE 13.3 Discrete Logistic Equations
Paper Fractional order logistic map Fractional order logistic map
(Wu and Baleanu, 2014) (El Raheem and Salman, 2014)
Recurrence x n11 5 xð0Þ x n11 5 x n 1 r: α ρx n ð1 2 x n Þ
relation 1 μ P n Γðn 2 j 1 vÞ Γð1 1 αÞ
ΓðvÞ j5n2m Γðn 2 j 1 1Þ x j ð1 2 x j Þ
Bifurcation
diagram

Ex:- Bifurcation for v 5 0:03 Ex:- Bifurcation for
ðα; rÞ 5 ð0:6; 0:25Þ

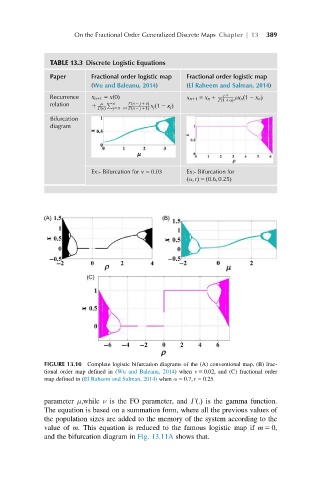
FIGURE 13.10 Complete logistic bifurcation diagrams of the (A) conventional map, (B) frac-
tional order map defined in (Wu and Baleanu, 2014) when v 5 0:02, and (C) fractional order
map defined in (El Raheem and Salman, 2014) when α 5 0:7; r 5 0:25.

parameter μ,while ν is the FO parameter, and Γð:Þ is the gamma function.
The equation is based on a summation form, where all the previous values of
the population sizes are added to the memory of the system according to the
value of m. This equation is reduced to the famous logistic map if m 5 0,
and the bifurcation diagram in Fig. 13.11A shows that.