Page 574 - Mathematical Techniques of Fractional Order Systems

548 Mathematical Techniques of Fractional Order Systems

(A) Chebyshev (B) Circle
2
CGWO 10 CGWO
CGOA
CGOA
Mean convergence curve 10 GOA Mean convergence curve 10 0 −2 GOA
GWO
GWO
0
10

−5
10
100 200 300 400 100 200 300 400
Iteration number Iteration number
(C) Gauss mouse (D) Iterative
2
10 CGWO CGWO
CGOA 0 CGOA
Mean convergence curve 10 0 −2 Mean convergence curve 10
GWO
GWO
GOA
GOA
10

100 200 300 400 100 200 300 400
Iteration number Iteration number
(E) Logistic (F) Piecewise
2
CGWO 10 CGWO
CGOA CGOA
Mean convergence curve Mean convergence curve 10 0 −2
GWO
GWO
0
10
GOA
GOA
10
10 −5
100 200 300 400 100 200 300 400
Iteration number Iteration number
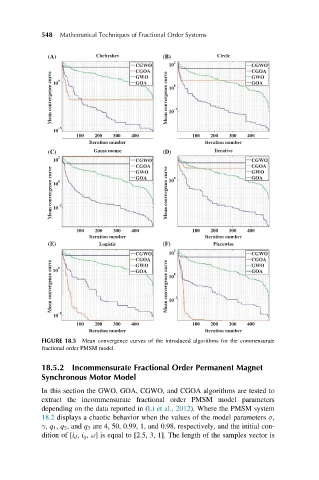
FIGURE 18.5 Mean convergence curves of the introduced algorithms for the commensurate
fractional order PMSM model.

18.5.2 Incommensurate Fractional Order Permanent Magnet
Synchronous Motor Model

In this section the GWO, GOA, CGWO, and CGOA algorithms are tested to
extract the incommensurate fractional order PMSM model parameters
depending on the data reported in (Li et al., 2012). Where the PMSM system
18.2 displays a chaotic behavior when the values of the model parameters σ,
γ, q 1 , q 2 , and q 3 are 4, 50, 0.99, 1, and 0.98, respectively, and the initial con-
dition of [i d , i q , ω] is equal to [2.5, 3, 1]. The length of the samples vector is