Page 575 - Mathematical Techniques of Fractional Order Systems

Parameters Identification of Fractional Order Chapter | 18 549

(G) Sine (H) Singer
2
CGWO 10 CGWO
CGOA CGOA
Mean convergence curve 10 Mean convergence curve 10 0
GWO
GWO
GOA
0
GOA

100 200 300 400 10 −2 100 200 300 400
Iteration number Iteration number
(I) (J)
Sinusoidal Tent
2 2
10 CGWO 10 CGWO
CGOA
CGOA
Mean convergence curve 10 0 GOA Mean convergence curve 10 0 −2 GOA
GWO
GWO
10
−2
10
100 200 300 400 100 200 300 400
Iteration number Iteration number
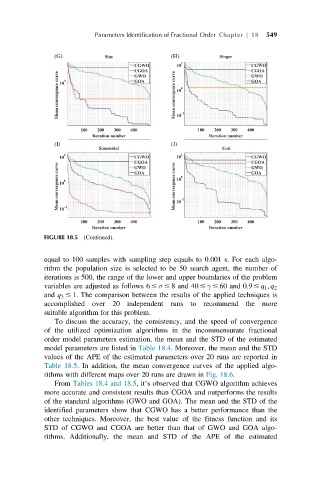
FIGURE 18.5 (Continued).

equal to 100 samples with sampling step equals to 0.001 s. For each algo-
rithm the population size is selected to be 50 search agent, the number of
iterations is 500, the range of the lower and upper boundaries of the problem
variables are adjusted as follows 6 # σ # 8 and 40 # γ # 60 and 0:9 # q 1 ; q 2
and q 3 # 1. The comparison between the results of the applied techniques is
accomplished over 20 independent runs to recommend the more
suitable algorithm for this problem.
To discuss the accuracy, the consistency, and the speed of convergence
of the utilized optimization algorithms in the incommensurate fractional
order model parameters estimation, the mean and the STD of the estimated
model parameters are listed in Table 18.4. Moreover, the mean and the STD
values of the APE of the estimated parameters over 20 runs are reported in
Table 18.5. In addition, the mean convergence curves of the applied algo-
rithms with different maps over 20 runs are drawn in Fig. 18.6.
From Tables 18.4 and 18.5, it’s observed that CGWO algorithm achieves
more accurate and consistent results than CGOA and outperforms the results
of the standard algorithms (GWO and GOA). The mean and the STD of the
identified parameters show that CGWO has a better performance than the
other techniques. Moreover, the best value of the fitness function and its
STD of CGWO and CGOA are better than that of GWO and GOA algo-
rithms. Additionally, the mean and STD of the APE of the estimated