Page 82 - Mathematical Techniques of Fractional Order Systems

70 Mathematical Techniques of Fractional Order Systems

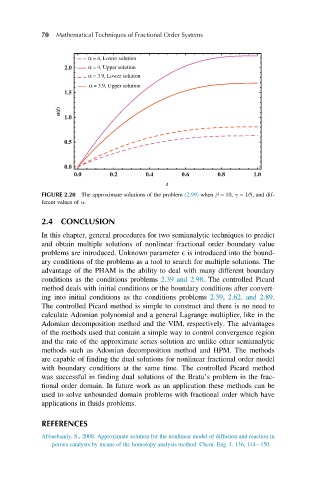
α = 4, Lower solution
2.0 α = 4, Upper solution
α = 3.9, Lower solution
α = 3.9, Upper solution
1.5

u(t)
1.0

0.5

0.0
0.0 0.2 0.4 0.6 0.8 1.0
t
FIGURE 2.20 The approximate solutions of the problem (2.99) when β 5 10, γ 5 1/5, and dif-
ferent values of α.

2.4 CONCLUSION
In this chapter, general procedures for two semianalytic techniques to predict
and obtain multiple solutions of nonlinear fractional order boundary value
problems are introduced. Unknown parameter E is introduced into the bound-
ary conditions of the problems as a tool to search for multiple solutions. The
advantage of the PHAM is the ability to deal with many different boundary
conditions as the conditions problems 2.39 and 2.98. The controlled Picard
method deals with initial conditions or the boundary conditions after convert-
ing into initial conditions as the conditions problems 2.39, 2.62, and 2.89.
The controlled Picard method is simple to construct and there is no need to
calculate Adomian polynomial and a general Lagrange multiplier, like in the
Adomian decomposition method and the VIM, respectively. The advantages
of the methods used that contain a simple way to control convergence region
and the rate of the approximate series solution are unlike other semianalytic
methods such as Adomian decomposition method and HPM. The methods
are capable of finding the dual solutions for nonlinear fractional order model
with boundary conditions at the same time. The controlled Picard method
was successful in finding dual solutions of the Bratu’s problem in the frac-
tional order domain. In future work as an application these methods can be
used to solve unbounded domain problems with fractional order which have
applications in fluids problems.

REFERENCES
Abbasbandy, S., 2008. Approximate solution for the nonlinear model of diffusion and reaction in
porous catalysts by means of the homotopy analysis method. Chem. Eng. J. 136, 144 150.