Page 78 - Mathematical Techniques of Fractional Order Systems

Nonlinear Fractional Order Boundary-Value Problems Chapter | 2 67

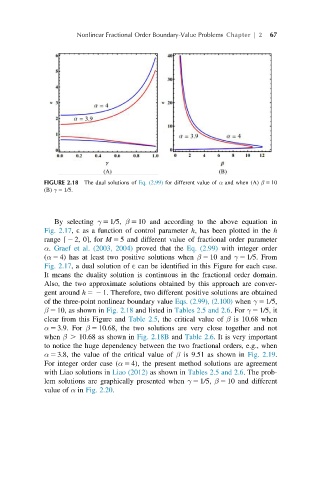
FIGURE 2.18 The dual solutions of Eq. (2.99) for different value of α and when (A) β 5 10
(B) γ 5 1/5.

By selecting γ 5 1/5, β 5 10 and according to the above equation in
Fig. 2.17, E as a function of control parameter h, has been plotted in the h
range [ 2 2, 0], for M 5 5 and different value of fractional order parameter
α. Graef et al. (2003, 2004) proved that the Eq. (2.99) with integer order
(α 5 4) has at least two positive solutions when β 5 10 and γ 5 1/5. From
Fig. 2.17, a dual solution of E can be identified in this Figure for each case.
It means the duality solution is continuous in the fractional order domain.
Also, the two approximate solutions obtained by this approach are conver-
gent around h 52 1. Therefore, two different positive solutions are obtained
of the three-point nonlinear boundary value Eqs. (2.99), (2.100) when γ 5 1/5,
β 5 10, as shown in Fig. 2.18 and listed in Tables 2.5 and 2.6.For γ 5 1/5, it
clear from this Figure and Table 2.5, the critical value of β is 10.68 when
α 5 3.9. For β 5 10.68, the two solutions are very close together and not
when β . 10.68 as shown in Fig. 2.18B and Table 2.6. It is very important
to notice the huge dependency between the two fractional orders, e.g., when
α 5 3.8, the value of the critical value of β is 9.51 as shown in Fig. 2.19.
For integer order case (α 5 4), the present method solutions are agreement
with Liao solutions in Liao (2012) as shown in Tables 2.5 and 2.6. The prob-
lem solutions are graphically presented when γ 5 1/5, β 5 10 and different
value of α in Fig. 2.20.