Page 74 - Mathematical Techniques of Fractional Order Systems

Nonlinear Fractional Order Boundary-Value Problems Chapter | 2 63

0.00030
Upper solution
0.00025 Lower solution

Absolute error 0.00020

0.00015

0.00010

0.00005

0.00000
0.0 0.2 0.4 0.6 0.8 1.0
t
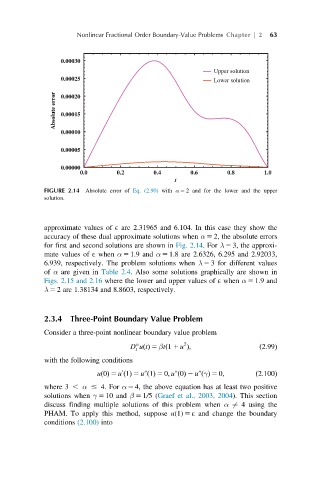
FIGURE 2.14 Absolute error of Eq. (2.90) with α 5 2 and for the lower and the upper
solution.

approximate values of E are 2.31965 and 6.104. In this case they show the
accuracy of these dual approximate solutions when α 5 2, the absolute errors
for first and second solutions are shown in Fig. 2.14.For λ 5 3, the approxi-
mate values of E when α 5 1.9 and α 5 1.8 are 2.6326, 6.295 and 2.92033,
6.939, respectively. The problem solutions when λ 5 3 for different values
of α are given in Table 2.4. Also some solutions graphically are shown in
Figs. 2.15 and 2.16 where the lower and upper values of E when α 5 1.9 and
λ 5 2 are 1.38134 and 8.8603, respectively.

2.3.4 Three-Point Boundary Value Problem

Consider a three-point nonlinear boundary value problem
α 2
D uðtÞ 5 βtð1 1 u Þ; ð2:99Þ
t
with the following conditions
0
uð0Þ 5 u ð1Þ 5 uvð1Þ 5 0; uvð0Þ 2 uvðγÞ 5 0; ð2:100Þ
where 3 , α # 4. For α 5 4, the above equation has at least two positive
solutions when γ 5 10 and β 5 1/5(Graef et al., 2003, 2004). This section
discuss finding multiple solutions of this problem when α 6¼ 4 using the
PHAM. To apply this method, suppose u(1) 5 E and change the boundary
conditions (2.100) into