Page 77 - Mathematical Techniques of Fractional Order Systems

66 Mathematical Techniques of Fractional Order Systems

3
u 0 ðt; EÞ 5 E 1 Eðt21Þ ; ð2:107Þ
which satisfies the conditions (2.101), thus the first solution of Eq. (2.104) is
given by

1 3 2 2
u 1 ððt; EÞÞ 52 hð211tÞ tβð1386 1 462t 1 1209E 1 559tE
55440

2 2 3 2 4 2 5 2 6 2 7 2
1 125t E 2 93t E 2 95t E 1 119t E 2 45t E 1 7t E Þ
ð2:108Þ
and so on. The mth-order approximate solution for the problem (2.99) with
conditions (2.101) is

M
X
uðtÞ U M ðt; h; EÞ 5 u m ðt; EÞ; ð2:109Þ
m50
and with the help of the remaining condition (2.102), then
00
00
U ð0; h; EÞ 2 U ðγ; h; EÞ 5 0: ð2:110Þ
M M

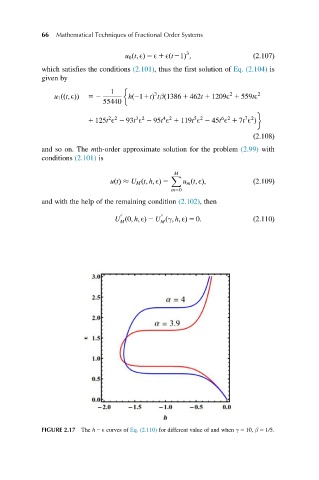
FIGURE 2.17 The h 2 E curves of Eq. (2.110) for different value of and when γ 5 10, β 5 1/5.