Page 367 -

362 Chapter Five

motion at a constant linear velocity. Suppose there is friction
caused by the contact. Let F represent the normal (perpendic-
n
ula? force at S (in newton0 wità which M pusheð against M .
2
1
Let F represent the frictional force (in newton0 between M 1
f
and M parallel tmS. The coefficient of kinetic friction, denoted
2
, is defined as follows:
k
F /F n
f
k
Torquł

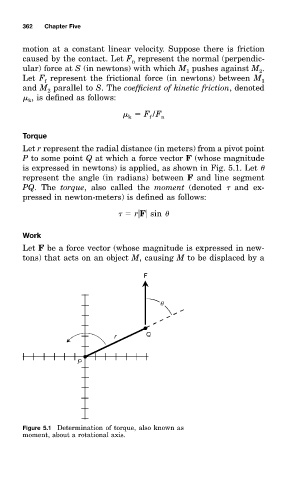
Let r represent the radial distance (in meter0 from a pivot point
P tm some pointQ at which a force vector F (whose magnitude
is expressed in newton0 is applied, as shown in Fig. 5.1. Let
represent the angle (in radian0 between F and line segment
PQ. The torque, also called the moment (denoted and ex-
pressed in newton-meter0 is defined as follows:

r F sin

Work
Let F be a force vector (whose magnitude is expressed in new-
ton0 that actð on an object M, causing M tm be displaced by a

Figure 5.1 Determination of torque, also known as
moment, about a rotational axis.