Page 168 - Matrix Analysis & Applied Linear Algebra

4.1 Spaces and Subspaces 163

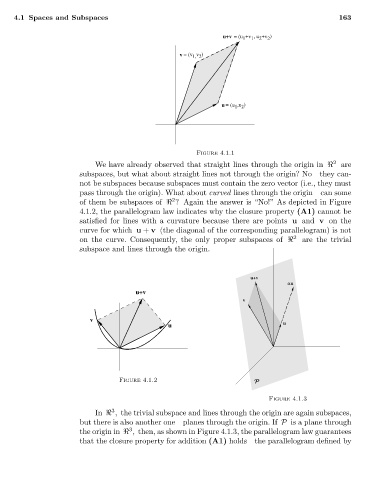
u+v = (u +v , u +v )
2
1
2
1
v = (v v )
1, 2

u = (u ,u )
1 2

Figure 4.1.1
2
We have already observed that straight lines through the origin in are
subspaces, but what about straight lines not through the origin? No—they can-
not be subspaces because subspaces must contain the zero vector (i.e., they must
pass through the origin). What about curved lines through the origin—can some
2
of them be subspaces of ? Again the answer is “No!” As depicted in Figure
4.1.2, the parallelogram law indicates why the closure property (A1) cannot be
satisfied for lines with a curvature because there are points u and v on the
curve for which u + v (the diagonal of the corresponding parallelogram) is not
2
on the curve. Consequently, the only proper subspaces of are the trivial
subspace and lines through the origin.

u+v
αu
u+v
v

v
u u

Figure 4.1.2 P

Figure 4.1.3
3
In , the trivial subspace and lines through the origin are again subspaces,
but there is also another one—planes through the origin. If P is a plane through
3
the origin in , then, as shown in Figure 4.1.3, the parallelogram law guarantees
that the closure property for addition (A1) holds—the parallelogram defined by