Page 244 - Matrix Analysis & Applied Linear Algebra

4.7 Linear Transformations 239

2
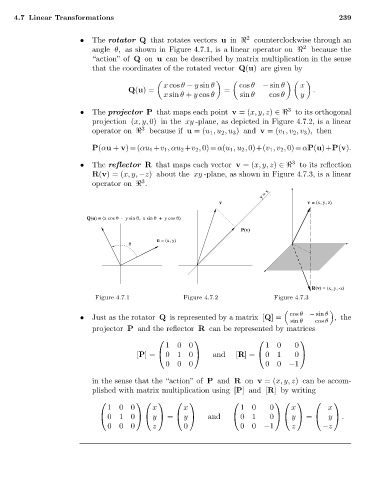
• The rotator Q that rotates vectors u in counterclockwise through an
2
angle θ, as shown in Figure 4.7.1, is a linear operator on because the
“action” of Q on u can be described by matrix multiplication in the sense
that the coordinates of the rotated vector Q(u) are given by

x cos θ − y sin θ cos θ − sin θ x
Q(u)= = .
x sin θ + y cos θ sin θ cos θ y
3
• The projector P that maps each point v =(x, y, z) ∈ to its orthogonal
projection (x, y, 0) in the xy -plane, as depicted in Figure 4.7.2, is a linear
3
operator on because if u =(u 1 ,u 2 ,u 3 ) and v =(v 1 ,v 2 ,v 3 ), then
P(αu + v)=(αu 1 +v 1 ,αu 2 +v 2 , 0)=α(u 1 ,u 2 , 0)+(v 1 ,v 2 , 0)=αP(u)+P(v).

3
• The reflector R that maps each vector v =(x, y, z) ∈ to its reflection
R(v)=(x, y, −z) about the xy -plane, as shown in Figure 4.7.3, is a linear
3
operator on .
y = x
v v = (x, y, z)

Q(u) = (x cos θ - y sin θ, x sin θ + y cos θ)
P(v)
u = (x, y)
θ

R(v) = (x, y, -z)
Figure 4.7.1 Figure 4.7.2 Figure 4.7.3

cos θ − sin θ
• Just as the rotator Q is represented by a matrix [Q]= , the
sin θ cos θ
projector P and the reflector R can be represented by matrices
   
100 10 0
[P]=  010  and [R]=  01 0 
000 00 −1

in the sense that the “action” of P and R on v =(x, y, z) can be accom-
plished with matrix multiplication using [P] and [R] by writing

           
100 x x 10 0 x x
010 y = y and 01 0 y = y .
           
000 z 0 00 −1 z −z