Page 56 - Mechanical Engineer's Data Handbook

STRENGTHS OF MATERIALS 45

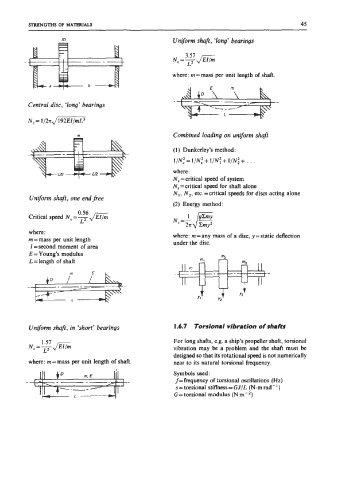
rn Uniform shaft, ‘long’ bearings
E
N,=F@ 3.57
1

where: m=mass per unit length of shaft.

Central disc, ‘long’ bearings

N, = 1/2ndm

m Combined loading on uniform shaft

(1) Dunkerley’s method:
1/N: = 1/N: + 1/N: + 1/Ni + , .

where:
N,=critical speed of system
N,=critical speed for shaft alone
N,, N,, etc.=critical speeds for discs acting alone
Uniform shaft, one endfree
(2) Energy method:
0 56
Critical speed N, =
L
where: where: m=any mass of a disc, y=static deflection
m=mass per unit length under the disc.
I =second moment of area
E = Young’s modulus
L=length of shaft

Uniform shaft, in ‘short’ bearings I .6.7 Torsional vibration of shafts

1.57
Nc’Fa For long shafts, e.g. a ship’s propeller shaft, torsional
vibration may be. a problem and the shaft must be
designed so that its rotational speed is not numerically
where: m=mass per unit length of shaft. near to its natural torsional frequency.
Symbols used:
j= frequency of torsional oscillations (Hz)
s=torsional stiffness=GJ/L (N-mrad-’)
G = torsional modulus (N m- *)