Page 346 - Mechanical Engineers' Handbook (Volume 2)

5 Approaches to Linear Systems Analysis 337

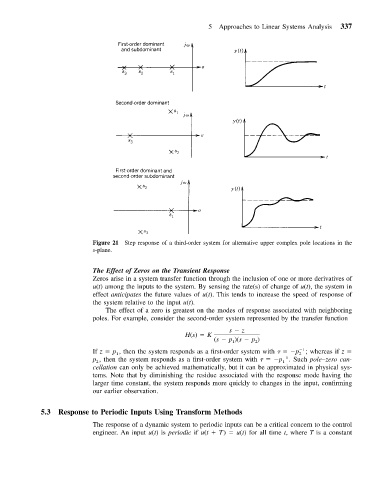
Figure 21 Step response of a third-order system for alternative upper complex pole locations in the
s-plane.

The Effect of Zeros on the Transient Response
Zeros arise in a system transfer function through the inclusion of one or more derivatives of
u(t) among the inputs to the system. By sensing the rate(s) of change of u(t), the system in
effect anticipates the future values of u(t). This tends to increase the speed of response of
the system relative to the input u(t).
The effect of a zero is greatest on the modes of response associated with neighboring
poles. For example, consider the second-order system represented by the transfer function
s z
H(s) K
(s p )(s p )
2
1
1
If z p , then the system responds as a first-order system with p ; whereas if z
1 2
1
p , then the system responds as a first-order system with p . Such pole–zero can-
1
2
cellation can only be achieved mathematically, but it can be approximated in physical sys-
tems. Note that by diminishing the residue associated with the response mode having the
larger time constant, the system responds more quickly to changes in the input, confirming
our earlier observation.
5.3 Response to Periodic Inputs Using Transform Methods
The response of a dynamic system to periodic inputs can be a critical concern to the control
engineer. An input u(t)is periodic if u(t T) u(t) for all time t, where T is a constant