Page 29 - Singiresu S. Rao-Mechanical Vibrations in SI Units, Global Edition-Pearson (2017)

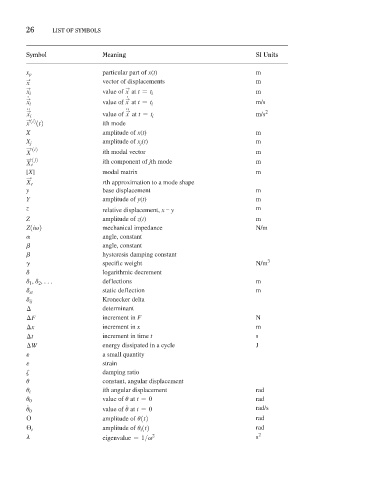
26 LISt oF SyMBoLS

Symbol Meaning SI Units

x p particular part of x(t) m
>
x vector of displacements m
>
>
x i value of x at t = t i m
> >
x ª value of x ª at t = t i m/s
i
> > 2
x ¶ value of x ¶ at t = t i m/s
i
>
x 1t2 ith mode
1i2
X amplitude of x(t) m
X j amplitude of x j (t) m
>
X 1i2 ith modal vector m
>
1 j2
X i ith component of jth mode m
[X] modal matrix m
>
X r rth approximation to a mode shape
y base displacement m
Y amplitude of y(t) m
z relative displacement, x – y m
Z amplitude of z(t) m
Z1iv2 mechanical impedance N/m
a angle, constant
b angle, constant
b hysteresis damping constant
g specific weight N/m 3
d logarithmic decrement
d 1 , d 2 , c deflections m
d st static deflection m
d ij Kronecker delta
∆ determinant
∆F increment in F N
∆x increment in x m
∆t increment in time t s
∆W energy dissipated in a cycle J
e a small quantity
e strain
z damping ratio
u constant, angular displacement
u i ith angular displacement rad
u 0 value of u at t = 0 rad
# #
u 0 value of u at t = 0 rad/s
ϴ amplitude of u1t2 rad
ϴ i amplitude of u i 1t2 rad
2
l eigenvalue = 1>v s 2