Page 140 - Mechanics Analysis Composite Materials

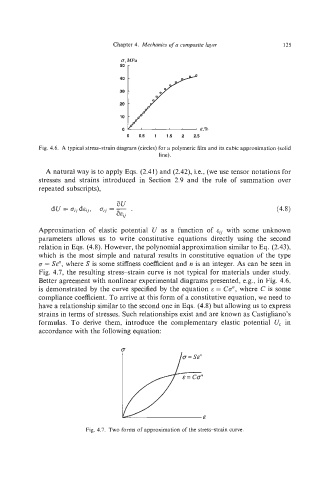
Chapter 4. Mechanics of a composite layer 125

E,%
0 05 1 1.5 2 2.5
Fig. 4.6. A typical stress-strain diagram (circles) for a polymeric film and its cubic approximation (solid
line).

A natural way is to apply Eqs. (2.41) and (2.42), i.e., (we use tensor notations for
stresses and strains introduced in Section 2.9 and the rule of summation over
repeated subscripts),

Approximation of elastic potential U as a function of eij with some unknown
parameters allows us to write constitutive equations directly using the second
relation in Eqs. (4.8). However, the polynomial approximation similar to Eq. (2.43),
which is the most simple and natural results in constitutive equation of the type
0 = SE",where S is some stiffness coefficient and n is an integer. As can be seen in
Fig. 4.7, the resulting stress-strain curve is not typical for materials under study.
Better agreement with nonlinear experimental diagrams presented, e.g., in Fig. 4.6,
is demonstrated by the curve specified by the equation E = CCY,where C is some
compliance coefficient. To arrive at this form of a constitutive equation, we need to
have a relationship similar to the second one in Eqs. (4.8) but allowing us to express
strains in terms of stresses. Such relationships exist and are known as Castigliano's
formulas. To derive them, introduce the complementary elastic potential U, in
accordance with the following equation:

Fig. 4.7. Two forms of approximation of the stress-strain curve.