Page 141 - Mechanics Analysis Composite Materials

126 Mechanics and analysis of composite materials

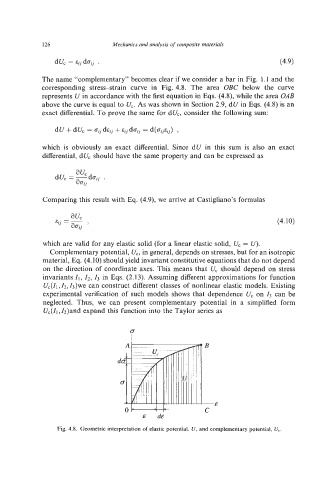
The name “complementary” becomes clear if we consider a bar in Fig. 1.1 and the
corresponding stress-strain curve in Fig. 4.8. The area OBC below the curve
represents U in accordance with the first equation in Eqs. (4.8), while the area OAB
above the curve is equal to U,. As was shown in Section 2.9, dU in Eqs. (4.8) is an
exact differential. To prove the same for dU,, consider the following sum:

which is obviously an exact differential. Since dU in this sum is also an exact
differential, dU, should have the same property and can be expressed as

Comparing this result with Eq. (4.9), we arrive at Castigliano’s formulas

(4.10)

which are valid for any elastic solid (for a linear elastic solid, U, = U).
Complementary potential, U,, in general, depends on stresses, but for an isotropic
material, Eq. (4.10) should yield invariant constitutive equations that do not depend
on the direction of coordinate axes. This means that U, should depend on stress
invariants 11~12, I3 in Eqs. (2.13). Assuming different approximations for function
Uc(Zl, Z2, I3)we can construct different classes of nonlinear elastic models. Existing
experimental verification of such models shows that dependence U, on 13 can be
neglected. Thus, we can present complementary potential in a simplified form
U, (ZI, Z2)and expand this function into the Taylor series as

E
C
E de
Fig. 4.8. Geometric interpretation of elastic potential. U. and complementary potential, U,.