Page 149 - Mechanics Analysis Composite Materials

134 Mechanics and analysis of composite materials
where the first term is linear, while the second term is a known function of
coordinates. Thus, we have another linear problem resolving which we find stresses,
calculate q2 and switch to the third step. This process is continued until the strains
corresponding to some step become close within the given accuracy to the results
found at the previous step.
Thus, the method of elastic solutions reduces the initial nonlinear problem to a
sequence of linear problems of the theory of elasticityfor the same material but with
some initial strains that can be transformed into initial stresses or additional loads.
This method readily provides a nonlinear solution for any problem that has a linear
solution, analytical or numerical. The main shortcoming of the method is its poor
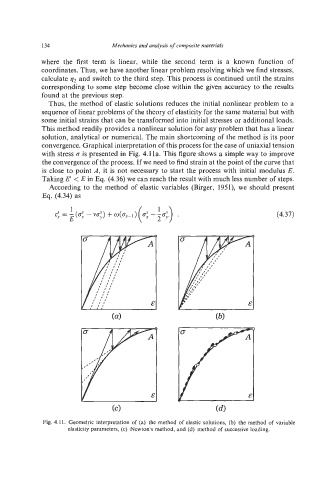
convergence. Graphical interpretation of this process for the case of uniaxial tension
with stress (r is presented in Fig. 4.1 la. This figure shows a simple way to improve
the convergence of the process. If we need to find strain at the point of the curve that
is close to point A, it is not necessary to start the process with initial modulus E.
Taking E' < E in Eq. (4.36)we can reach the result with much less number of steps.
According to the method of elastic variables (Birger, 1951), we should present
Eq. (4.34) as

(4.37)

Fig. 4.1 1. Geometric interpretation of (a) the method of elastic solutions, (b) the method of variable
elasticity parameters, (c) Newton's method, and (d) method of successive loading.