Page 147 - Mechanics Analysis Composite Materials

132 Mechanics and analysis of composite materials

accordance with Eq. (4.21).To do this, we need to know the plastic Poisson's ratio
vp that can be found as vp = -E,,/&,. Using Eqs. (4.29) and (4.30) we arrive at

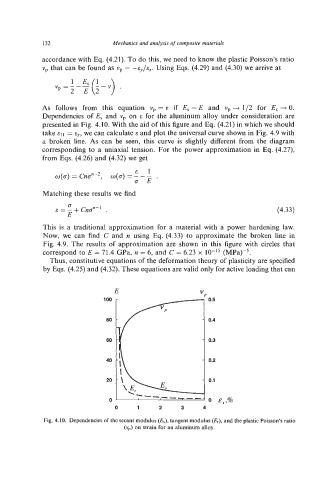
As follows from this equation vp = v if E, =E and vp + 112 for E, +0.
Dependencies of Es and vp on E for the aluminum alloy under consideration are
presented in Fig. 4.10. With the aid of this figure and Eq. (4.21) in which we should
take 81 I = E,, we can calculate E and plot the universal curve shown in Fig. 4.9 with
a broken line. As can be seen, this curve is slightly different from the diagram
corresponding to a uniaxial tension. For the power approximation in Eq. (4.27),
from Eqs. (4.26) and (4.32) we get

E l
a(.) = - --
0 E'
Matching these results we find

E = -+ Cncrn-' . (4.33)
E
This is a traditional approximation for a material with a power hardening law.
Now, we can find C and n using Eq. (4.33) to approximate the broken line in
Fig. 4.9. The results of approximation are shown in this figure with circles that
correspond to E = 71.4 GPa, n = 6, and C = 6.23 x (MPa)-5.
Thus, constitutive equations of the deformation theory of plasticity are specified
by Eqs. (4.25) and (4.32).These equations are valid only for active loading that can

E
"D
100 0.5

80 0.4

60 0.3

40 09

20 0.1

0 0 E,
0 1 2 3 4
Fig. 4.10. Dependenciesof the secant modulus (Es),tangent modulus (Et), and the plastic Poisson's ratio
(v,) on strain for an aluminum alloy.