Page 241 - Mechanics Analysis Composite Materials

226 Mechanics and analysis of composite materials

z

X

*v
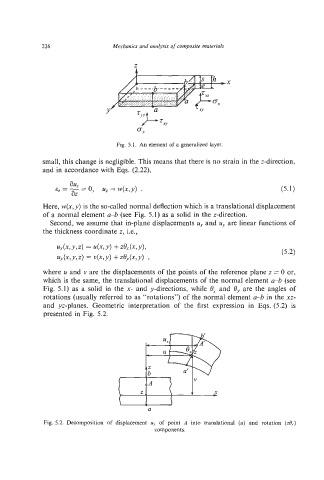
Fig. 5.1. An element of a generalized layer.

small, this change is negligible. This means that there is no strain in the z-direction,
and in accordance with Eqs. (2.22),

(5.1)

Here, w(x,y)is the so-called normal deflection which is a translational displacement
of a normal element a-b (see Fig. 5.1) as a solid in the z-direction.
Second, we assume that in-plane displacements u, and u, are linear functions of
the thickness coordinate z, i.e.,

where u and v are the displacements of the points of the reference plane z = 0 or,
which is the same, the translational displacements of the normal element a-6 (see
Fig. 5.1) as a solid in the x- and y-directions, while 0, and 0, are the angles of
rotations (usually referred to as “rotations”) of the normal element ab in the xz-
and yz-planes. Geometric interpretation of the first expression in Eqs. (5.2) is
presented in Fig. 5.2.

a

Fig. 5.2. Decomposition of displacement u, of point A into translational (u) and rotation (z&)
components.