Page 327 - Mechanics of Asphalt Microstructure and Micromechanics

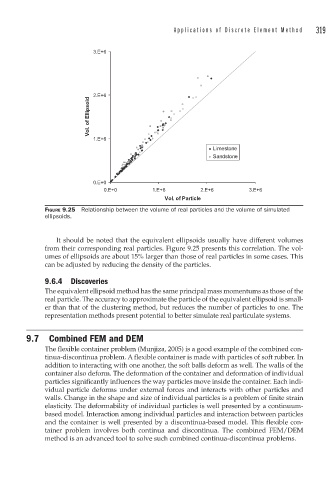
Applications of Discrete Element Method 319

3.E+6

2.E+6
Vol. of Ellipsoid

1.E+6
Limestone
Sandstone

0.E+0
0.E+0 1.E+6 2.E+6 3.E+6
Vol. of Particle
FIGURE 9.25 Relationship between the volume of real particles and the volume of simulated
ellipsoids.

It should be noted that the equivalent ellipsoids usually have different volumes
from their corresponding real particles. Figure 9.25 presents this correlation. The vol-
umes of ellipsoids are about 15% larger than those of real particles in some cases. This
can be adjusted by reducing the density of the particles.

9.6.4 Discoveries
The equivalent ellipsoid method has the same principal mass momentums as those of the
real particle. The accuracy to approximate the particle of the equivalent ellipsoid is small-
er than that of the clustering method, but reduces the number of particles to one. The
representation methods present potential to better simulate real particulate systems.

9.7 Combined FEM and DEM
The flexible container problem (Munjiza, 2005) is a good example of the combined con-
tinua-discontinua problem. A flexible container is made with particles of soft rubber. In
addition to interacting with one another, the soft balls deform as well. The walls of the
container also deform. The deformation of the container and deformation of individual
particles significantly influences the way particles move inside the container. Each indi-
vidual particle deforms under external forces and interacts with other particles and
walls. Change in the shape and size of individual particles is a problem of finite strain
elasticity. The deformability of individual particles is well presented by a continuum-
based model. Interaction among individual particles and interaction between particles
and the container is well presented by a discontinua-based model. This flexible con-
tainer problem involves both continua and discontinua. The combined FEM/DEM
method is an advanced tool to solve such combined continua-discontinua problems.