Page 150 - Microtectonics

5.6 · Microscopic Shear Sense Indicators in Mylonite 139

Box 5.4 Continued

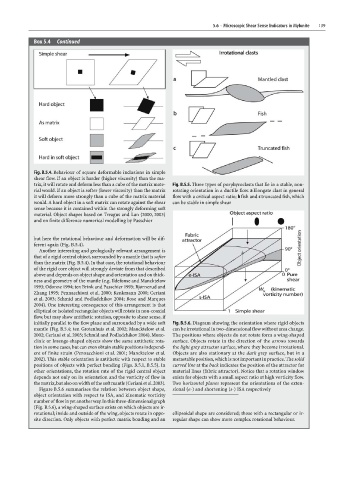
Fig. B.5.4. Behaviour of square deformable inclusions in simple
shear flow. If an object is harder (higher viscosity) than the ma-
trix, it will rotate and deform less than a cube of the matrix mate- Fig. B.5.5. Three types of porphyroclasts that lie in a stable, non-
rial would. If an object is softer (lower viscosity) than the matrix rotating orientation in a ductile flow. a Elongate clast in general
it will deform more strongly than a cube of the matrix material flow with a critical aspect ratio; b fish and c truncated fish, which
would. A hard object in a soft matrix can rotate against the shear can be stable in simple shear
sense because it is contained within the strongly deforming soft
material. Object shapes based on Treagus and Lan (2000, 2003)
and on finite difference numerical modelling by Passchier

but here the rotational behaviour and deformation will be dif-
ferent again (Fig. B.5.4).
Another interesting and geologically relevant arrangement is
that of a rigid central object, surrounded by a mantle that is softer
than the matrix (Fig. B.5.4). In that case, the rotational behaviour
of the rigid core object will strongly deviate from that described
above and depends on object shape and orientation and on thick-
ness and geometry of the mantle (e.g. Ildefonse and Mancktelow
1993; Odonne 1994; ten Brink and Passchier 1995; Bjørnerud and
Zhang 1995; Pennacchioni et al. 2000; Kenkmann 2000; Ceriani
et al. 2003; Schmid and Podladchikov 2004; Bose and Marques
2004). One interesting consequence of this arrangement is that
elliptical or isolated rectangular objects will rotate in non-coaxial
flow, but may show antithetic rotation, opposite to shear sense, if
initially parallel to the flow plane and surrounded by a wide soft Fig. B.5.6. Diagram showing the orientation where rigid objects
mantle (Fig. B.5.4; ten Grotenhuis et al. 2002; Mancktelow et al. can be irrotational in two-dimensional flow without area change.
2002; Ceriani et al. 2003; Schmid and Podladchikov 2004). Mono- The positions where objects do not rotate form a wing-shaped
clinic or lozenge-shaped objects show the same antithetic rota- surface. Objects rotate in the direction of the arrows towards
tion in some cases, but can even obtain stable positions independ- the light grey attractor surface, where they become irrotational.
ent of finite strain (Pennacchioni et al. 2001; Mancktelow et al. Objects are also stationary at the dark grey surface, but in a
2002). This stable orientation is antithetic with respect to stable metastable position, which is not important in practice. The solid
positions of objects with perfect bonding (Figs. B.5.1, B.5.5). In curved line at the back indicates the position of the attractor for
other orientations, the rotation rate of the rigid central object material lines (fabric attractor). Notice that a rotation window
depends not only on its orientation and the vorticity of flow in exists for objects with a small aspect ratio at high vorticity flow.
the matrix, but also on width of the soft mantle (Ceriani et al. 2003). Two horizontal planes represent the orientations of the exten-
Figure B.5.6 summarises the relation between object shape, sional (e-) and shortening (s-) ISA respectively
object orientation with respect to ISA, and kinematic vorticity
number of flow in yet another way. In this three-dimensional graph
(Fig. B.5.6), a wing-shaped surface exists on which objects are ir-
rotational; inside and outside of the wing, objects rotate in oppo- ellipsoidal shape are considered; those with a rectangular or ir-
site direction. Only objects with perfect matrix bonding and an regular shape can show more complex rotational behaviour.