Page 36 - Microtectonics

2.12 · Rheology 23
rocks. The stress exponent n is known as the strain-
rate sensitivity of the flow stress and is 1 for Newtonian
behaviour and higher than one for power-law behaviour,
though not usually exceeding 5 for rocks. Although there
are exceptions, Newtonian flow is thought to represent
diffusion-accommodated processes (including pressure
solution; Sects. 3.3, 3.8), while power-law flow is typical
of processes involving dislocation creep (Sect. 3.4). In
simple cases, rocks show steady state flow, meaning
that, if the differential stress is not varied, they will de-
form at a constant strain rate. The ductile strength of
rocks generally decreases with increasing depth in the
crust if other factors do not change. Mean stress does
not have much influence on the ductile rheology of rocks.
However, grain size can under many circumstances be
important (Sect. 3.8).
Most rocks do not show steady state flow during the
entire deformation history because the fabric of the rock
changes with progressive deformation. Both strain hard-
ening and strain softening behaviour occur in rocks
(Fig. 2.12). In Fig. 2.12 strain hardening and softening are
indicated for constant strain rate, as may happen in an
experiment. In nature, hardening may be a process of de-
creasing strain rate and increasing differential stress and
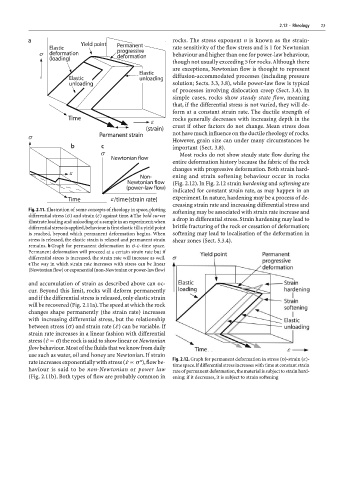
Fig. 2.11. Illustration of some concepts of rheology in space, plotting softening may be associated with strain rate increase and
differential stress (σ) and strain (ε) against time. a The bold curves
illustrate loading and unloading of a sample in an experiment; when a drop in differential stress. Strain hardening may lead to
differential stress is applied, behaviour is first elastic till a yield point brittle fracturing of the rock or cessation of deformation;
is reached, beyond which permanent deformation begins. When softening may lead to localisation of the deformation in
stress is released, the elastic strain is relaxed and permanent strain shear zones (Sect. 5.3.4).
remains. b Graph for permanent deformation in σ-ε-time space.
Permanent deformation will proceed at a certain strain rate but if
differential stress is increased, the strain rate will increase as well.
c The way in which strain rate increases with stress can be linear
(Newtonian flow) or exponential (non-Newtonian or power-law flow)

and accumulation of strain as described above can oc-
cur. Beyond this limit, rocks will deform permanently
and if the differential stress is released, only elastic strain
will be recovered (Fig. 2.11a). The speed at which the rock
changes shape permanently (the strain rate) increases
with increasing differential stress, but the relationship
between stress (σ) and strain rate (Ü) can be variable. If
strain rate increases in a linear fashion with differential
stress (Ü ∝ σ) the rock is said to show linear or Newtonian
flow behaviour. Most of the fluids that we know from daily
use such as water, oil and honey are Newtonian. If strain
n
rate increases exponentially with stress (Ü ∝ σ ), flow be- Fig. 2.12. Graph for permanent deformation in stress (σ)-strain (ε)-
time space. If differential stress increases with time at constant strain
haviour is said to be non-Newtonian or power law rate of permanent deformation, the material is subject to strain hard-
(Fig. 2.11b). Both types of flow are probably common in ening; if it decreases, it is subject to strain softening