Page 231 - MODELING OF ASPHALT CONCRETE

Unified Disturbed State Constitutive Modeling of Asphalt Concr ete 209

by Bonaquist (1996) and Bonaquist and Witczak (1997). This chapter contains the DSC
model, which includes the HISS model as a special case. It is considered to be unified
and economical compared to other models currently available.

Objective
The main objective of this chapter is to present a full mechanistic approach with the
powerful and unified constitutive models based on the disturbed state concept (DSC)
that has been already developed, and can be readily used for modeling asphalt concrete
and pavement applications. Before the presentation of the DSC models and associated
two- and three-dimensional codes for the treatment of various distresses, a brief review
of some of the available models is first presented.

Review of RM Approach
The resilient modulus (RM) approach has been used extensively in pavement engineering
(Witczak and Uzan 1988; Barksdale et al. 1990; Huang 1993). Although it can provide
satisfactory predictions of elastic uniaxial displacements, it is not capable of predicting
the foregoing multidimensional effects such as rutting, microcracking, and fracture.
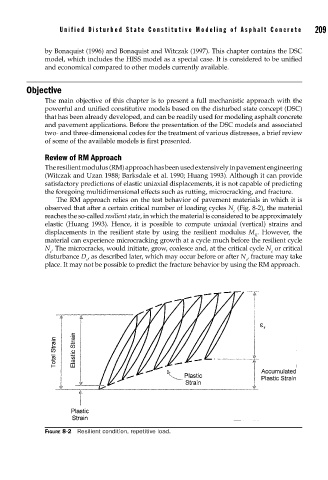
The RM approach relies on the test behavior of pavement materials in which it is
observed that after a certain critical number of loading cycles N (Fig. 8-2), the material
c
reaches the so-called resilient state, in which the material is considered to be approximately
elastic (Huang 1993). Hence, it is possible to compute uniaxial (vertical) strains and
displacements in the resilient state by using the resilient modulus M . However, the
R
material can experience microcracking growth at a cycle much before the resilient cycle
N . The microcracks, would initiate, grow, coalesce and, at the critical cycle N or critical
c c
disturbance D , as described later, which may occur before or after N , fracture may take
c c
place. It may not be possible to predict the fracture behavior by using the RM approach.

FIGURE 8-2 Resilient condition, repetitive load.