Page 70 - Modelling in Transport Phenomena A Conceptual Approach

3.3. MASS TRANSFER COEFFICIENT 51

Equation (3.3-5) can be generalized in the form

(3.3-7)

where AM is the mass transfer area and (AcA),, is the characteristic concentration
difference.

3.3.1 Physical Interpretation of Mass Transfer Coefficient
The use of Fick’s first law of diffusion, Eq. (2.1-9), in Eq. (3.3-2) gives

(3.3-8)

Combination of Eqs. (3.3-4) and (3.3-8) gives

The convection mass transfer coefficient can be determined from Eq. (3.3-9) if the
diffusion coefficient, the overall concentration difference, and the concentration
gradient at the wall are known. Since the calculation of the concentration gradient
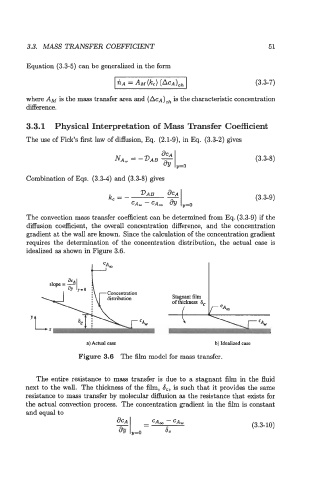
requires the determination of the concentration distribution, the actual case is
idealized as shown in Figure 3.6.

a) Actual case b) Idealized case
Figure 3.6 The film model for mass transfer.

The entire resistance to mass transfer is due to a stagnant film in the fluid
next to the wall. The thickness of the film, 6,, is such that it provides the same
resistance to mass transfer by molecular diffusion as the resistance that exists for
the actual convection process. The concentration gradient in the film is constant
and equal to
CA, - CAW (3.3-10)
6,