Page 371 - MODERN ELECTROCHEMISTRY

ION–ION INTERACTIONS 307

increasing r because the volume of the spherical shell increases as It follows
from these considerations that goes through a minimum for a particular, critical
value of r. This conclusion may also be reached by computing the number of ions in
a series of shells, each of an arbitrarily selected thickness of 0.01 nm (Table 3.15).

3.8.3. The Fraction of Ion Pairs, According to Bjerrum
If one integrates between a lower and an upper limit, one gets the probability
of finding a negative ion within a distance from the reference positive ion, defined
by the limits. Now, for two oppositely charged ions to stick together to form an ion
pair, it is necessary that they should be close enough for the Coulombic attractive
energy to overcome the thermal energy that scatters them apart. Let this “close-
enough” distance be q. Then one can say that an ion pair will form when the distance
r between a positive and a negative ion becomes less than q. Thus, the probability of
ion-pair formation is given by the integral of between a lower limit of a, the distance
of closest approach of ions, and an upper limit of q.
Now, the probability of any particular event is the number of times that the
particular event is expected to be observed divided by the total number of observations.
Hence, the probability of ion-pair formation is the number of ions of species i that are
associated into ion pairs divided by the total number of i ions; i.e., the probability of
ion-pair formation is the fraction of ions that are associated into ion pairs. Thus,

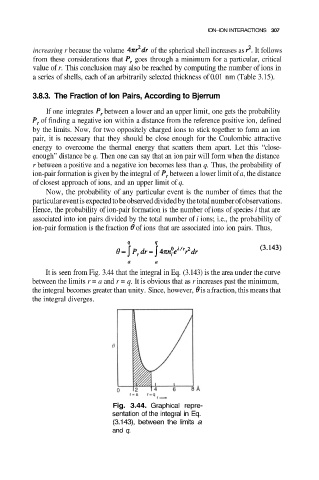
It is seen from Fig. 3.44 that the integral in Eq. (3.143) is the area under the curve
between the limits r = a and r = q. It is obvious that as r increases past the minimum,
the integral becomes greater than unity. Since, however, is a fraction, this means that
the integral diverges.

Fig. 3.44. Graphical repre-
sentation of the integral in Eq.
(3.143), between the limits a
and q.