Page 205 - Modern Optical Engineering The Design of Optical Systems

188 Chapter Nine

practice, the acceptable blur diameter B is usually determined empiri-
cally by examining a series of defocused images to decide the level of
acceptability; the equations above are then fitted to the results.

9.9 Diffraction Effects of Apertures
Even if we assume that an infinitely small point source of light is
possible, no lens system can form a true point image, even though the
lens be perfectly made and absolutely free of aberrations. This results
from the fact that light does not really travel in straight-line rays, but
behaves as a wave motion, bending around corners and obstructions to
a small but finite degree.
According to Huygen’s principle of light-wave propagation, each point
on a wave front may be considered as a source of spherical wavelets;
these wavelets reinforce or interfere with each other to form the new
wave front. When the original wave front is infinite in extent, the new
wave front is simply the envelope of the wavelets in the direction of
propagation.
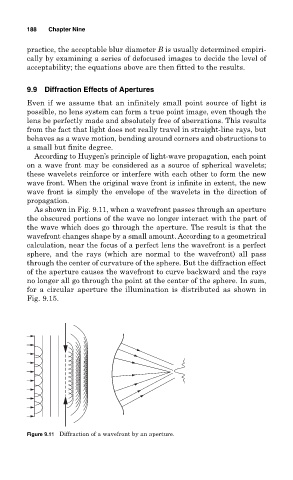
As shown in Fig. 9.11, when a wavefront passes through an aperture
the obscured portions of the wave no longer interact with the part of
the wave which does go through the aperture. The result is that the
wavefront changes shape by a small amount. According to a geometrical
calculation, near the focus of a perfect lens the wavefront is a perfect
sphere, and the rays (which are normal to the wavefront) all pass
through the center of curvature of the sphere. But the diffraction effect
of the aperture causes the wavefront to curve backward and the rays
no longer all go through the point at the center of the sphere. In sum,
for a circular aperture the illumination is distributed as shown in
Fig. 9.15.

Figure 9.11 Diffraction of a wavefront by an aperture.