Page 197 - Book Hosokawa Nanoparticle Technology Handbook

3.8 SIMULATION OF COLLOIDAL DISPERSION SYSTEM FUNDAMENTALS

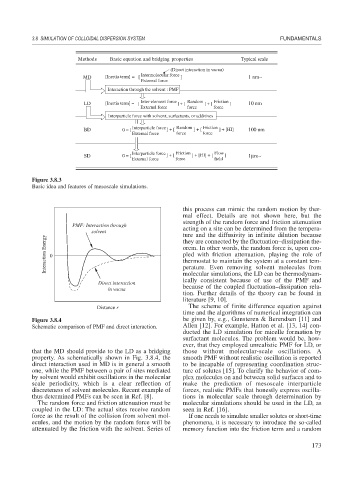
Methods Basic equation and bridging properties Typical scale
(Direct interaction in vacua)
Intermolecular force
MD [Inertia term] =[ ] 1 nm∼
External force
Interaction through the solvent : PMF
LD [Inertia term] = [ Inter-element force ] + [ Random ] + [ Friction ] 10 nm
External force force force
Interparticle force with solvent, surfactants, or additives

Interparticle force Random Friction
BD 0 = [ ] + [ ] + [ ] + [HI] 100 nm
External force force force

Interparticle force Friction Flow
SD 0= [ ] + [ ] + [HI] + [ ] 1μm∼
External force force field

Figure 3.8.3
Basic idea and features of mesoscale simulations.

this process can mimic the random motion by ther-
mal effect. Details are not shown here, but the
strength of the random force and friction attenuation
PMF: Interaction through acting on a site can be determined from the tempera-
solvent ture and the diffusivity in infinite dilution because
Interaction Energy 0 orem. In other words, the random force is, upon cou-
they are connected by the fluctuation–dissipation the-
pled with friction attenuation, playing the role of
thermostat to maintain the system at a constant tem-
perature. Even removing solvent molecules from
molecular simulations, the LD can be thermodynam-
ically consistent because of use of the PMF and
Direct interaction
in vacua because of the coupled fluctuation–dissipation rela-
tion. Further details of the theory can be found in
literature [9, 10].
Distance r The scheme of finite difference equation against
time and the algorithms of numerical integration can
Figure 3.8.4 be given by, e.g., Gunsteren & Berendsen [11] and
Schematic comparison of PMF and direct interaction. Allen [12]. For example, Hatton et al. [13, 14] con-
ducted the LD simulation for micelle formation by
surfactant molecules. The problem would be, how-
ever, that they employed unrealistic PMF for LD, or
that the MD should provide to the LD as a bridging those without molecular-scale oscillations. A
property. As schematically shown in Fig. 3.8.4, the smooth PMF without realistic oscillation is reported
direct interaction used in MD is in general a smooth to be incapable of representing coordination struc-
one, while the PMF between a pair of sites mediated ture of solutes [15]. To clarify the behavior of com-
by solvent would exhibit oscillations in the molecular plex molecules on and between solid surfaces and to
scale periodicity, which is a clear reflection of make the prediction of mesoscale interparticle
discreteness of solvent molecules. Recent example of forces, realistic PMFs that honestly express oscilla-
thus determined PMFs can be seen in Ref. [8]. tions in molecular scale through determination by
The random force and friction attenuation must be molecular simulations should be used in the LD, as
coupled in the LD: The actual sites receive random seen in Ref. [16].
force as the result of the collision from solvent mol- If one needs to simulate smaller solutes or short-time
ecules, and the motion by the random force will be phenomena, it is necessary to introduce the so-called
attenuated by the friction with the solvent. Series of memory function into the friction term and a random

173