Page 212 - Numerical Analysis and Modelling in Geomechanics

BACK ANALYSIS OF GEOTECHNICAL PROBLEMS 193

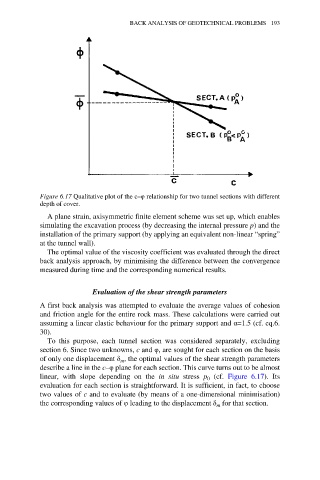
Figure 6.17 Qualitative plot of the c–φ relationship for two tunnel sections with different
depth of cover.
A plane strain, axisymmetric finite element scheme was set up, which enables
simulating the excavation process (by decreasing the internal pressure p) and the
installation of the primary support (by applying an equivalent non-linear “spring”
at the tunnel wall).
The optimal value of the viscosity coefficient was evaluated through the direct
back analysis approach, by minimising the difference between the convergence
measured during time and the corresponding numerical results.

Evaluation of the shear strength parameters
A first back analysis was attempted to evaluate the average values of cohesion
and friction angle for the entire rock mass. These calculations were carried out
assuming a linear elastic behaviour for the primary support and α=1.5 (cf. eq.6.
30).
To this purpose, each tunnel section was considered separately, excluding
section 6. Since two unknowns, c and φ, are sought for each section on the basis
of only one displacement δ , the optimal values of the shear strength parameters
m
describe a line in the c–φ plane for each section. This curve turns out to be almost
linear, with slope depending on the in situ stress p 0 (cf. Figure 6.17). Its
evaluation for each section is straightforward. It is sufficient, in fact, to choose
two values of c and to evaluate (by means of a one-dimensional minimisation)
the corresponding values of φ leading to the displacement δ for that section.
m