Page 251 - Numerical Analysis and Modelling in Geomechanics

232 SEISMIC MICROZONING USING NUMERICAL MODELLING

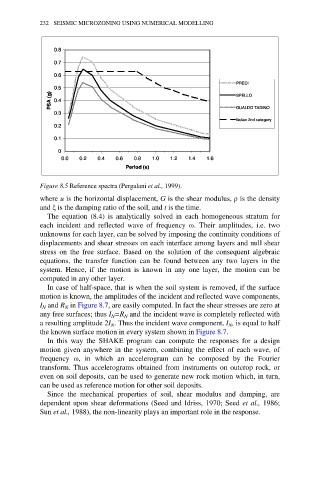
Figure 8.5 Reference spectra (Pergalani et al., 1999).
where u is the horizontal displacement, G is the shear modulus, ρ is the density
and ξ is the damping ratio of the soil, and t is the time.
The equation (8.4) is analytically solved in each homogeneous stratum for
each incident and reflected wave of frequency ω. Their amplitudes, i.e. two
unknowns for each layer, can be solved by imposing the continuity conditions of
displacements and shear stresses on each interface among layers and null shear
stress on the free surface. Based on the solution of the consequent algebraic
equations, the transfer function can be found between any two layers in the
system. Hence, if the motion is known in any one layer, the motion can be
computed in any other layer.
In case of half-space, that is when the soil system is removed, if the surface
motion is known, the amplitudes of the incident and reflected wave components,
I and R in Figure 8.7, are easily computed. In fact the shear stresses are zero at
N
N
any free surfaces; thus I =R and the incident wave is completely reflected with
N
N
a resulting amplitude 2I . Thus the incident wave component, I , is equal to half
N
N
the known surface motion in every system shown in Figure 8.7.
In this way the SHAKE program can compute the responses for a design
motion given anywhere in the system, combining the effect of each wave, of
frequency ω, in which an accelerogram can be composed by the Fourier
transform. Thus accelerograms obtained from instruments on outcrop rock, or
even on soil deposits, can be used to generate new rock motion which, in turn,
can be used as reference motion for other soil deposits.
Since the mechanical properties of soil, shear modulus and damping, are
dependent upon shear deformations (Seed and Idriss, 1970; Seed et al., 1986;
Sun et al., 1988), the non-linearity plays an important role in the response.