Page 362 - Numerical Analysis and Modelling in Geomechanics

RESERVOIR COMPACTION, SUBSIDENCE AND WELL DAMAGE 343

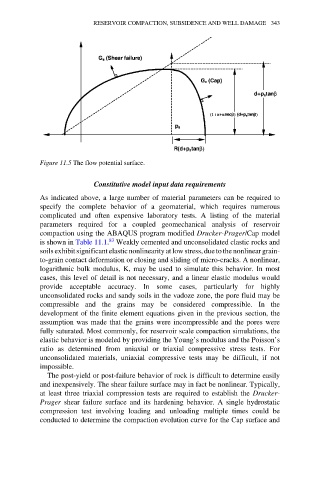
Figure 11.5 The flow potential surface.

Constitutive model input data requirements
As indicated above, a large number of material parameters can be required to
specify the complete behavior of a geomaterial, which requires numerous
complicated and often expensive laboratory tests. A listing of the material
parameters required for a coupled geomechanical analysis of reservoir
compaction using the ABAQUS program modified Drucker-Prager/Cap model
83
is shown in Table 11.1. Weakly cemented and unconsolidated clastic rocks and
soils exhibit significant elastic nonlinearity at low stress, due to the nonlinear grain-
to-grain contact deformation or closing and sliding of micro-cracks. A nonlinear,
logarithmic bulk modulus, K, may be used to simulate this behavior. In most
cases, this level of detail is not necessary, and a linear elastic modulus would
provide acceptable accuracy. In some cases, particularly for highly
unconsolidated rocks and sandy soils in the vadoze zone, the pore fluid may be
compressible and the grains may be considered compressible. In the
development of the finite element equations given in the previous section, the
assumption was made that the grains were incompressible and the pores were
fully saturated. Most commonly, for reservoir scale compaction simulations, the
elastic behavior is modeled by providing the Young’s modulus and the Poisson’s
ratio as determined from uniaxial or triaxial compressive stress tests. For
unconsolidated materials, uniaxial compressive tests may be difficult, if not
impossible.
The post-yield or post-failure behavior of rock is difficult to determine easily
and inexpensively. The shear failure surface may in fact be nonlinear. Typically,
at least three triaxial compression tests are required to establish the Drucker-
Prager shear failure surface and its hardening behavior. A single hydrostatic
compression test involving loading and unloading multiple times could be
conducted to determine the compaction evolution curve for the Cap surface and