Page 369 - Numerical Methods for Chemical Engineering

358 7 Probability theory and stochastic simulation

a

1 1
1 1
er er
2 2
site n 2 site n 2

attice attice

1 1 2 2 1 1 2 2
attice site n er attice site n er

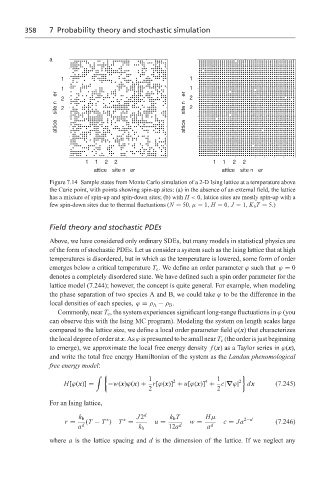
Figure 7.14 Sample states from Monte Carlo simulation of a 2-D Ising lattice at a temperature above
the Curie point, with points showing spin-up sites: (a) in the absence of an external field, the lattice
has a mixture of spin-up and spin-down sites; (b) with H < 0, lattice sites are mostly spin-up with a
few spin-down sites due to thermal fluctuations (N = 50,µ = 1, H = 0, J = 1, K b T = 5.)

Field theory and stochastic PDEs
Above, we have considered only ordinary SDEs, but many models in statistical physics are
of the form of stochastic PDEs. Let us consider a system such as the Ising lattice that at high
temperatures is disordered, but in which as the temperature is lowered, some form of order
emerges below a critical temperature T c . We define an order parameter ϕ such that ϕ = 0
denotes a completely disordered state. We have defined such a spin order parameter for the
lattice model (7.244); however, the concept is quite general. For example, when modeling
the phase separation of two species A and B, we could take ϕ to be the difference in the
local densities of each species, ϕ = ρ A − ρ B .
Commonly, near T c , the system experiences significant long-range fluctuations in ϕ (you
can observe this with the Ising MC program). Modeling the system on length scales large
compared to the lattice size, we define a local order parameter field ϕ(x) that characterizes
the local degree of order at x.As ϕ is presumed to be small near T c (the order is just beginning
to emerge), we approximate the local free energy density f (x) as a Taylor series in ϕ(x),
and write the total free energy Hamiltonian of the system as the Landau phenomological
free energy model:
' 1
1 2 4 1 2
H[ϕ(x)] = −w(x)ϕ(x) + r[ϕ(x)] + u[ϕ(x)] + c|∇ϕ| dx (7.245)
2 2
For an Ising lattice,

k b J2 d k b T Hµ 2−d
∗
∗
r = (T − T ) T = u = w = c = Ja (7.246)
a d k b 12a d a d
where a is the lattice spacing and d is the dimension of the lattice. If we neglect any