Page 312 - Origin and Prediction of Abnormal Formation Pressures

PORE WATER COMPACTION CHEMISTRY AS RELATED TO OVERPRESSURES 281
0.6
m
Xo =0.5
0 m So = 0.25
E 0
oE 0.4- _ ......

~ ~ ~ jmcl

0.2

0
0L5 1
Volume of suspension, I
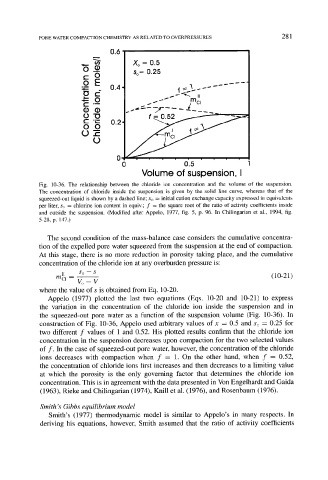
Fig. 10-36. The relationship between the chloride ion concentration and the volume of the suspension.
The concentration of chloride inside the suspension is given by the solid line curve, whereas that of the
squeezed-out liquid is shown by a dashed line; Xo -- initial cation exchange capacity expressed in equivalents
per liter, so = chlorine ion content in equiv.; f = the square root of the ratio of activity coefficients inside
and outside the suspension. (Modified after Appelo, 1977, fig. 5, p. 96. In Chilingarian et al., 1994, fig.
5-28, p. 147.)

The second condition of the mass-balance case considers the cumulative concentra-
tion of the expelled pore water squeezed from the suspension at the end of compaction.
At this stage, there is no more reduction in porosity taking place, and the cumulative
concentration of the chloride ion at any overburden pressure is:
So - s (10-21)
m~l= V0- V
where the value of s is obtained from Eq. 10-20.
Appelo (1977) plotted the last two equations (Eqs. 10-20 and 10-21) to express
the variation in the concentration of the chloride ion inside the suspension and in
the squeezed-out pore water as a function of the suspension volume (Fig. 10-36). In
construction of Fig. 10-36, Appelo used arbitrary values of x = 0.5 and So = 0.25 for
two different f values of 1 and 0.52. His plotted results confirm that the chloride ion
concentration in the suspension decreases upon compaction for the two selected values
of f. In the case of squeezed-out pore water, however, the concentration of the chloride
ions decreases with compaction when f = 1. On the other hand, when f = 0.52,
the concentration of chloride ions first increases and then decreases to a limiting value
at which the porosity is the only governing factor that determines the chloride ion
concentration. This is in agreement with the data presented in Von Engelhardt and Gaida
(1963), Rieke and Chilingarian (1974), Knill et al. (1976), and Rosenbaum (1976).

Smith's Gibbs equilibrium model
Smith's (1977) thermodynamic model is similar to Appelo's in many respects. In
deriving his equations, however, Smith assumed that the ratio of activity coefficients