Page 61 - PRINCIPLES OF QUANTUM MECHANICS as Applied to Chemistry and Chemical Physics
P. 61
52 Schro Èdinger wave mechanics
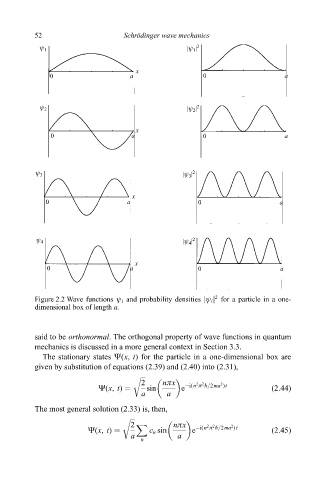
ψ 1 |ψ | 2
1
x
0 a 0 a
ψ 2 |ψ | 2
2
x
0 a 0 a
ψ 3 |ψ 3 | 2
x
0 a 0 a
ψ 4 |ψ | 2
4
x
0 a 0 a
2
Figure 2.2 Wave functions ø i and probability densities jø i j for a particle in a one-
dimensional box of length a.
said to be orthonormal. The orthogonal property of wave functions in quantum
mechanics is discussed in a more general context in Section 3.3.
The stationary states Ø(x, t) for the particle in a one-dimensional box are
given by substitution of equations (2.39) and (2.40) into (2.31),
r
2 nðx ÿi(n ð "=2ma )t
2
2 2
Ø(x, t) sin e (2:44)
a a
The most general solution (2.33) is, then,
r
2 X nðx ÿi(n ð "=2ma )t
2
2 2
Ø(x, t) c n sin e (2:45)
a a
n