Page 181 - Petroleum Geology

158

is n7rd3/6, and they occupy (1 - f) of the bulk volume, where f is the frac
tional porosity. So the ratio of surface area to bulk volume, known as the
specific surface, is approximated by:
S 6(1 - f)/d. (8.1)
The saturation due to a film of water of thickness t around the grains is ap-
proximated by:
sWa Y 6t(l- f)/fd. (8.2)
If we consider a reservoir rock consisting of spherical grains of 75 pm dia-
meter, corresponding to fine sand, 26% porosity, and an irreducible water
saturation of 5%, eq. 8.2 suggests that the film of water, if evenly distributed
about the grains, would be about 0.2 pm thick. If the water saturation were
20%, the film thickness would be about 1 pm.
The question now arises, what is the thickness of an adsorbed film of water?
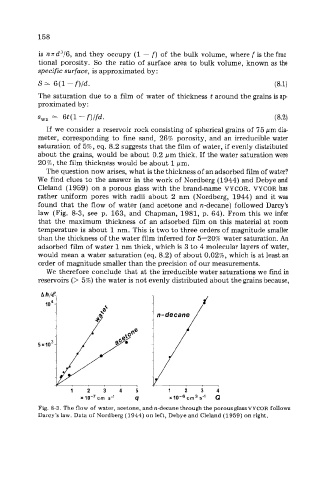
We find clues to the answer in the work of Nordberg (1944) and Debye and
Cleland (1959) on a porous glass with the brand-name VYCOR. VYCOR has
rather uniform pores with radii about 2 nm (Nordberg, 1944) and it was
found that the flow of water (and acetone and n-decane) followed Darcy’s
law (Fig. 8-3, see p. 163, and Chapman, 1981, p. 64). From this we infer
that the maximum thickness of an adsorbed film on this material at room
temperature is about 1 nm. This is two to three orders of magnitude smaller
than the thickness of the water film inferred for 5-20% water saturation. An
adsorbed film of water 1 nm thick, which is 3 to 4 molecular layers of water,
would mean a water saturation (eq. 8.2) of about 0.02%, which is at least an
order of magnitude smaller than the precision of our measurements.
We therefore conclude that at the irreducible water saturations we find in
1
reservoirs (> 5%) the water is not evenly distributed about the grains because,

n-decane

1 2 3 4 5 1 2 3 4
~10-~cm q xIO-~ cm3 s1 Q
s-1
Fig. 8-3. The flow of water, acetone, and n-decane through the porousglass VYCOR follows
Darcy’s law. Data of Nordberg (1944) on left, Debye and Cleland (1959) on right.