Page 187 - Petroleum Geology

164

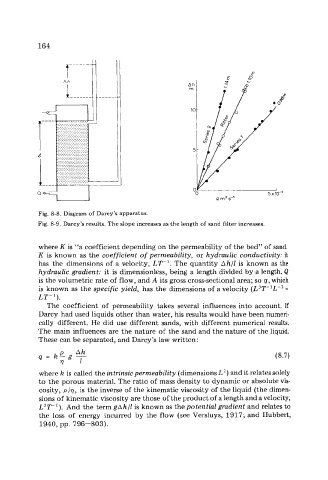
Fig. 8-8. Diagram of Darcy’s apparatus.
Fig. 8-9. Darcy’s results. The slope increases as the length of sand filter increases,

where K is “a coefficient depending on the permeability of the bed” of sand.
K is known as the coefficient of permeability, or hydraulic conductivity: it
has the dimensions of a velocity, LT-’. The quantity Ah11 is known as the
hydraulic gradient: it is dimensionless, being a length divided by a length. Q
is the volumetric rate of flow, and A its gross cross-sectional area; so q, which
is known as the specific yield, has the dimensions of a velocity (L3T-‘L-2 =
LT-’).
The coefficient of permeability takes several influences into account. If
Darcy had used liquids other than water, his results would have been numeri-
cally different. He did use different sands, with different numerical results.
The main influences are the nature of the sand and the nature of the liquid.
These can be separated, and Darcy’s law written:

where h is called the intrinsic permeability (dimensions L2) and it relates solely
to the porous material. The ratio of mass density to dynamic or absolute vis-
cosity, p/q, is the inverse of the kinematic viscosity of the liquid (the dimen-
sions of kinematic viscosity are those of the product of a length and a velocity,
L’T- I). And the term gAh/l is known as the potential gradient and relates to
the loss of energy incurred by the flow (see Versluys, 1917; and Hubbert,
1940, pp. 796-803).