Page 207 - Phase Space Optics Fundamentals and Applications

188 Chapter Five

MTF (μ/Ω = 0.02, p = 12)
MTF (μ/Ω = 0)

1
1 0.8
0.8 0.6
0.6 H
H 0.4 0.4
0.2 0.2
0 0 0 0
0 0
0.5 0.5 0.5 0.5
1 1 1 1
W 20 /λ 1.5 1.5 ν/Ω W 20 /λ 1.5 1.5 ν/Ω
2 2 2
(a) (b)
MTF (μ/Ω = 0.06, p = 12)
MTF (μ/Ω = 0.3, p = 12)

1 1
0.8 0.8
H 0.6 H 0.6
0.4 0.4
0.2 0.2
0 0
0 0 0
0.5 0.5 0.5 0
1 1 0.5
W 20 /λ 1 W 20 /λ 1
1.5 1.5 ν/Ω 1.5 1.5 ν/Ω
2 2
(c) (d)
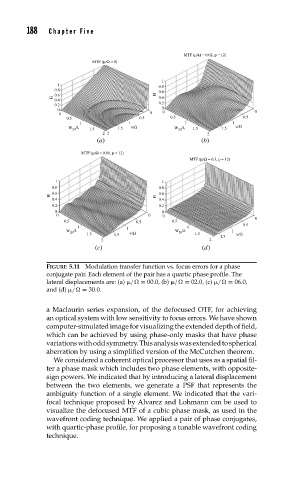
FIGURE 5.11 Modulation transfer function vs. focus errors for a phase
conjugate pair. Each element of the pair has a quartic phase profile. The
lateral displacements are: (a) / = 00.0, (b) / = 02.0, (c) / = 06.0,
and (d) / = 30.0.

a Maclaurin series expansion, of the defocused OTF, for achieving
an optical system with low sensitivity to focus errors. We have shown
computer-simulated image for visualizing the extended depth of field,
which can be achieved by using phase-only masks that have phase
variationswithoddsymmetry.Thisanalysiswasextendedtospherical
aberration by using a simplified version of the McCutchen theorem.
We considered a coherent optical processor that uses as a spatial fil-
ter a phase mask which includes two phase elements, with opposite-
sign powers. We indicated that by introducing a lateral displacement
between the two elements, we generate a PSF that represents the
ambiguity function of a single element. We indicated that the vari-
focal technique proposed by Alvarez and Lohmann can be used to
visualize the defocused MTF of a cubic phase mask, as used in the
wavefront coding technique. We applied a pair of phase conjugates,
with quartic-phase profile, for proposing a tunable wavefront coding
technique.