Page 101 - Physical Principles of Sedimentary Basin Analysis

4.1 Rock compressibility 83

5 4

compressibility x 10 −10 [1/Pa] 3 2 α α s bc α pc α pp

0 1 α bp
0.00 0.05 0.10 0.15 0.20 0.25 0.30
φ [−]
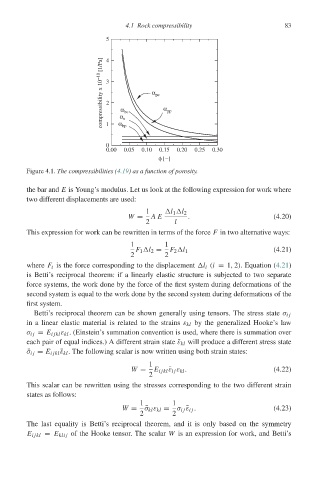
Figure 4.1. The compressibilities (4.19) as a function of porosity.

the bar and E is Young’s modulus. Let us look at the following expression for work where
two different displacements are used:
1 l 1 l 2
W = AE . (4.20)
2 l
This expression for work can be rewritten in terms of the force F in two alternative ways:
1 1
F 1 l 2 = F 2 l 1 (4.21)
2 2
where F i is the force corresponding to the displacement l i (i = 1, 2). Equation (4.21)
is Betti’s reciprocal theorem: if a linearly elastic structure is subjected to two separate
force systems, the work done by the force of the first system during deformations of the
second system is equal to the work done by the second system during deformations of the
first system.
Betti’s reciprocal theorem can be shown generally using tensors. The stress state σ ij
in a linear elastic material is related to the strains ε kl by the generalized Hooke’s law
σ ij = E ijkl ε kl . (Einstein’s summation convention is used, where there is summation over
each pair of equal indices.) A different strain state ¯ε kl will produce a different stress state
¯ σ ij = E ijkl ¯ε kl . The following scalar is now written using both strain states:
1
W = E ijkl ¯ε ij ε kl . (4.22)
2
This scalar can be rewritten using the stresses corresponding to the two different strain
states as follows:
1 1
W = ¯ σ kl ε kl = σ ij ¯ε ij . (4.23)
2 2
The last equality is Betti’s reciprocal theorem, and it is only based on the symmetry
E ijkl = E kli j of the Hooke tensor. The scalar W is an expression for work, and Betti’s