Page 182 - Physical Principles of Sedimentary Basin Analysis

164 Heat flow

The temperature equation (6.226) is linear and we can therefore add together solutions to
make a new solution. We just have to make sure that the new solution fulfills the boundary
conditions and the initial condition. The following example shows how a sill solution can
be added to a solution T n (z, t) for the temperature in absence of sills. If a sill of thickness a 1
intrudes the depth z 1 at time t 1 with a temperature T 1 we then have that the temperature is

(z − z 1 ) (t − t 1 )

T (z, t) = T n (z, t) + T 1 − T n (z 1 , t 1 ) T ˆ , (6.238)
a t 0
for t ≥ t 1 , where t 0 is the characteristic time for the sill. The temperature T n (z 1 , t 1 ) has
to be subtracted from the sill temperature T 1 in front of the T -function in order to fulfill
ˆ
the initial condition T (z 1 , t 1 ) = T 1 . The sill-solution has zero (or almost zero) temperature
a long distance away from the sill, and the addition of a sill solution does not alter any
boundary condition far away. The same reasoning can be applied to handle several sills at
the same time or at a later time.
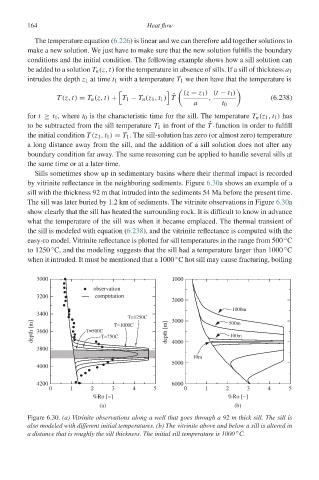
Sills sometimes show up in sedimentary basins where their thermal impact is recorded
by vitrinite reflectance in the neighboring sediments. Figure 6.30a shows an example of a
sill with the thickness 92 m that intruded into the sediments 54 Ma before the present time.
The sill was later buried by 1.2 km of sediments. The vitrinite observations in Figure 6.30a
show clearly that the sill has heated the surrounding rock. It is difficult to know in advance
what the temperature of the sill was when it became emplaced. The thermal transient of
the sill is modeled with equation (6.238), and the vitrinite reflectance is computed with the
◦
easy-ro model. Vitrinite reflectance is plotted for sill temperatures in the range from 500 C
◦
◦
to 1250 C, and the modeling suggests that the sill had a temperature larger than 1000 C
◦
when it intruded. It must be mentioned that a 1000 C hot sill may cause fracturing, boiling
3000 1000
observation
3200 computation
2000
1000m
3400
T=1250C 3000 500m
depth [m] 3600 T=500C T=750C depth [m] 100m
T=1000C

3800 4000
10m
5000
4000

4200 6000
0 1 2 3 4 5 0 1 2 3 4 5
%Ro [−] %Ro [−]
(a) (b)
Figure 6.30. (a) Vitrinite observations along a well that goes through a 92 m thick sill. The sill is
also modeled with different initial temperatures. (b) The vitrinite above and below a sill is altered in
a distance that is roughly the sill thickness. The initial sill temperature is 1000 C.
◦