Page 185 - Physical Principles of Sedimentary Basin Analysis

6.16 Solidification and latent heat of fusion 167

3

2

1
3 1.4 0.6 0.2 0
^ z 0

−1

−2

−3
0.0 0.2 0.4 0.6 0.8 1.0
^ t
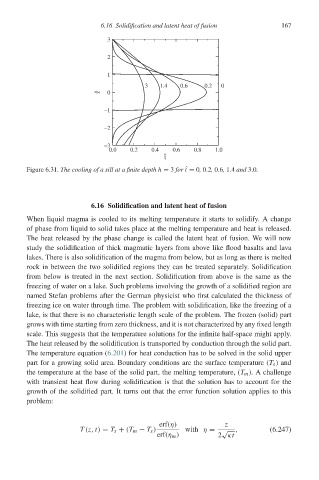
Figure 6.31. The cooling of a sill at a finite depth h = 3 for ˆ t = 0, 0.2, 0.6, 1.4 and 3.0.

6.16 Solidification and latent heat of fusion
When liquid magma is cooled to its melting temperature it starts to solidify. A change
of phase from liquid to solid takes place at the melting temperature and heat is released.
The heat released by the phase change is called the latent heat of fusion. We will now
study the solidification of thick magmatic layers from above like flood basalts and lava
lakes. There is also solidification of the magma from below, but as long as there is melted
rock in between the two solidified regions they can be treated separately. Solidification
from below is treated in the next section. Solidification from above is the same as the
freezing of water on a lake. Such problems involving the growth of a solidified region are
named Stefan problems after the German physicist who first calculated the thickness of
freezing ice on water through time. The problem with solidification, like the freezing of a
lake, is that there is no characteristic length scale of the problem. The frozen (solid) part
grows with time starting from zero thickness, and it is not characterized by any fixed length
scale. This suggests that the temperature solutions for the infinite half-space might apply.
The heat released by the solidification is transported by conduction through the solid part.
The temperature equation (6.201) for heat conduction has to be solved in the solid upper
part for a growing solid area. Boundary conditions are the surface temperature (T s ) and
the temperature at the base of the solid part, the melting temperature, (T m ). A challenge
with transient heat flow during solidification is that the solution has to account for the
growth of the solidified part. It turns out that the error function solution applies to this
problem:

erf(η) z
T (z, t) = T s + (T m − T s ) with η = √ , (6.247)
erf(η m ) 2 κt