Page 189 - Physical Principles of Sedimentary Basin Analysis

6.17 Solidification of sills and dikes 171

directly from equation (6.253). If the sill has the thickness 2a then we have that the sill is
solidified when z m (t s ) =−a, which gives

a 2
t s = . (6.259)
4κη 2 m
2
A sill has the characteristic length scale, a, and the characteristic time scale t 0 = a /κ.
The dimensionless time when solidification is complete is therefore
1
ˆ t s = . (6.260)
4η 2 m
Both the temperature solution and the position of the liquid/solid interface can be written
in a dimensionless form. The dimensionless temperature solution is
√
T − T 0 erfc(ˆz/2 ˆ t)
ˆ
T = = (6.261)
T m − T 0 erfc(−η m )
where the dimensionless version of z m is

ˆ z m (ˆ t) =−2η m t. (6.262)
ˆ
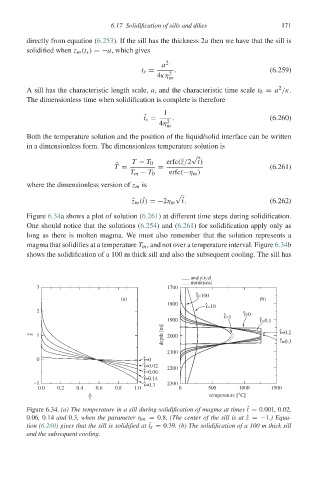
Figure 6.34a shows a plot of solution (6.261) at different time steps during solidification.
One should notice that the solutions (6.254) and (6.261) for solidification apply only as
long as there is molten magma. We must also remember that the solution represents a
magma that solidifies at a temperature T m , and not over a temperature interval. Figure 6.34b
shows the solidification of a 100 m thick sill and also the subsequent cooling. The sill has

analytical
numerical
3 1700
^ t=100
(a) (b)
1800 ^ t=10
2 ^
^ t=1 t=0
1900 ^ t=0.1
^ z 1 depth [m] 2000 ^ t=0.2
^
t=0.3
2100
0 ^ t=0
^ t=0.02
^ t=0.06 2200
^ t=0.14
−1 ^ t=0.3 2300
0.0 0.2 0.4 0.6 0.8 1.0 0 500 1000 1500
^ temperature [°C]
T
Figure 6.34. (a) The temperature in a sill during solidification of magma at times ˆ t = 0.001, 0.02,
0.06, 0.14 and 0.3, when the parameter η m = 0.8. (The center of the sill is at ˆz =−1.) Equa-
tion (6.260) gives that the sill is solidified at ˆ t s = 0.39. (b) The solidification of a 100 m thick sill
and the subsequent cooling.