Page 194 - Physical Principles of Sedimentary Basin Analysis

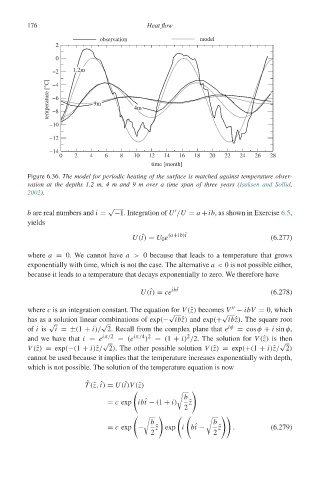
176 Heat flow

observation model
2
0
−2 1.2m
temperature [°C] −6 9m 4m
−4

−8
−10
−12

−14
0 2 4 6 8 10 12 14 16 18 20 22 24 26 28
time [month]
Figure 6.36. The model for periodic heating of the surface is matched against temperature obser-
vation at the depths 1.2 m, 4 m and 9 m over a time span of three years (Isaksen and Sollid,
2002).
√

b are real numbers and i = −1. Integration of U /U = a +ib, as shown in Exercise 6.5,
yields
(a+ib)ˆ t
U(ˆ t) = U 0 e (6.277)
where a = 0. We cannot have a > 0 because that leads to a temperature that grows
exponentially with time, which is not the case. The alternative a < 0 is not possible either,
because it leads to a temperature that decays exponentially to zero. We therefore have

U(ˆ t) = ce ibˆ t (6.278)

where c is an integration constant. The equation for V (ˆz) becomes V − ibV = 0, which
√ √
has as a solution linear combinations of exp(− ibˆz) and exp(+ ibˆz). The square root
√ √
of i is i =±(1 + i)/ 2. Recall from the complex plane that e iφ = cos φ + i sin φ,
) = (1 + i) /2. The solution for V (ˆz) is then
and we have that i = e iπ/2 = (e iπ/4 2 2
√ √
V (ˆz) = exp(−(1 + i)ˆz/ 2). The other possible solution V (ˆz) = exp(+(1 + i)ˆz/ 2)
cannot be used because it implies that the temperature increases exponentially with depth,
which is not possible. The solution of the temperature equation is now
ˆ
T (ˆz, ˆ t) = U(ˆ t)V (ˆz)

b
= c exp ibˆ t − (1 + i) ˆ z
2

b b
= c exp − ˆ z exp i bˆ t − ˆ z . (6.279)
2 2