Page 261 - Physical Principles of Sedimentary Basin Analysis

7.14 Backstripping and tectonic subsidence 243

Δ
w(t) water
water y(t)

s(t) sedimentary basin

crust c
c crust

mantle
a 2
a 1 mantle

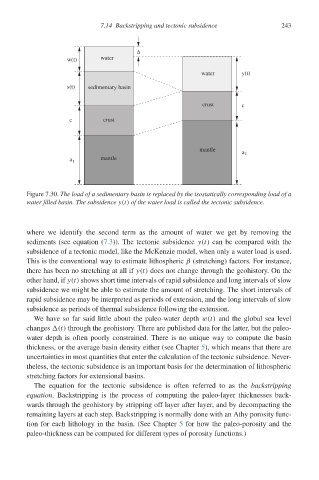
Figure 7.30. The load of a sedimentary basin is replaced by the isostatically corresponding load of a
water filled basin. The subsidence y(t) of the water load is called the tectonic subsidence.

where we identify the second term as the amount of water we get by removing the
sediments (see equation (7.3)). The tectonic subsidence y(t) can be compared with the
subsidence of a tectonic model, like the McKenzie model, when only a water load is used.
This is the conventional way to estimate lithospheric β (stretching) factors. For instance,
there has been no stretching at all if y(t) does not change through the geohistory. On the
other hand, if y(t) shows short time intervals of rapid subsidence and long intervals of slow
subsidence we might be able to estimate the amount of stretching. The short intervals of
rapid subsidence may be interpreted as periods of extension, and the long intervals of slow
subsidence as periods of thermal subsidence following the extension.
We have so far said little about the paleo-water depth w(t) and the global sea level
changes (t) through the geohistory. There are published data for the latter, but the paleo-
water depth is often poorly constrained. There is no unique way to compute the basin
thickness, or the average basin density either (see Chapter 5), which means that there are
uncertainties in most quantities that enter the calculation of the tectonic subsidence. Never-
theless, the tectonic subsidence is an important basis for the determination of lithospheric
stretching factors for extensional basins.
The equation for the tectonic subsidence is often referred to as the backstripping
equation. Backstripping is the process of computing the paleo-layer thicknesses back-
wards through the geohistory by stripping off layer after layer, and by decompacting the
remaining layers at each step. Backstripping is normally done with an Athy porosity func-
tion for each lithology in the basin. (See Chapter 5 for how the paleo-porosity and the
paleo-thickness can be computed for different types of porosity functions.)