Page 259 - Physical Principles of Sedimentary Basin Analysis

7.13 Thermal subsidence of the oceanic lithosphere 241

1
2

depth [km] 3

4

5

6
−1200 −1000 −800 −600 −400 −200 0 200 400 600 800 1000
distance [km]
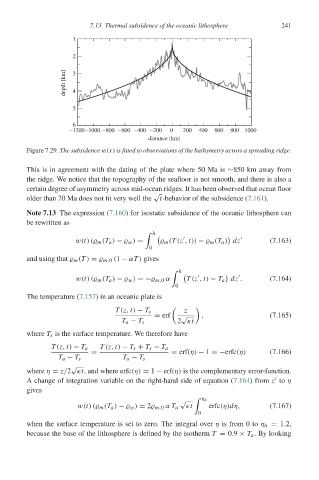
Figure 7.29. The subsidence w(x) is fitted to observations of the bathymetry across a spreading ridge.

This is in agreement with the dating of the plate where 50 Ma is ∼850 km away from
the ridge. We notice that the topography of the seafloor is not smooth, and there is also a
certain degree of asymmetry across mid-ocean ridges. It has been observed that ocean floor
√
older than 70 Ma does not fit very well the t-behavior of the subsidence (7.161).
Note 7.13 The expression (7.160) for isostatic subsidence of the oceanic lithosphere can
be rewritten as

h

w(t) ( m (T a ) − w ) = m (T (z , t)) − m (T a ) dz (7.163)
0
and using that m (T ) = m,0 (1 − αT ) gives
h

w(t) ( m (T a ) − w ) =− m,0 α T (z , t) − T a dz . (7.164)
0
The temperature (7.157) in an oceanic plate is

T (z, t) − T s z
= erf √ , (7.165)
T a − T s 2 κt
where T s is the surface temperature. We therefore have

T (z, t) − T a T (z, t) − T s + T s − T a
= = erf(η) − 1 =−erfc(η) (7.166)
T a − T s T a − T s
√
where η = z/2 κt, and where erfc(η) = 1 − erf(η) is the complementary error-function.

A change of integration variable on the right-hand side of equation (7.164) from z to η
gives
√ η h
w(t) ( m (T a ) − w ) = 2 m,0 α T a κt erfc(η)dη, (7.167)
0
when the surface temperature is set to zero. The integral over η is from 0 to η h = 1.2,
because the base of the lithosphere is defined by the isotherm T = 0.9 × T a . By looking