Page 258 - Physical Principles of Sedimentary Basin Analysis

240 Subsidence

plate subsidence
0
0
200
5
400
600
depth [km] 800
10

15
1000
plate thickness
20

1200
25
0 20 40 60 80 100
distance [km]
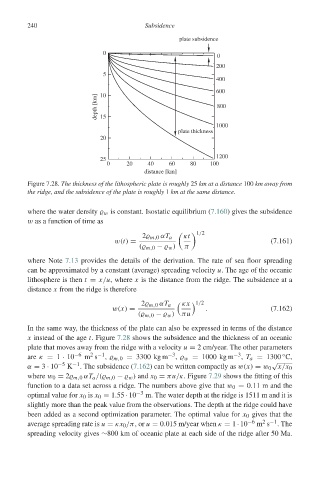
Figure 7.28. The thickness of the lithospheric plate is roughly 25 km at a distance 100 km away from
the ridge, and the subsidence of the plate is roughly 1 km at the same distance.

where the water density w is constant. Isostatic equilibrium (7.160) gives the subsidence
w as a function of time as

1/2
2 m,0 αT a κt
w(t) = (7.161)
( m,0 − w ) π
where Note 7.13 provides the details of the derivation. The rate of sea floor spreading
can be approximated by a constant (average) spreading velocity u. The age of the oceanic
lithosphere is then t = x/u, where x is the distance from the ridge. The subsidence at a
distance x from the ridge is therefore

2 m,0 αT a
κx 1/2
w(x) = . (7.162)
( m,0 − w ) πu
In the same way, the thickness of the plate can also be expressed in terms of the distance
x instead of the age t. Figure 7.28 shows the subsidence and the thickness of an oceanic
plate that moves away from the ridge with a velocity u = 2 cm/year. The other parameters
2 −1
are κ = 1 · 10 −6 m s , m,0 = 3300 kg m −3 , w = 1000 kg m −3 , T a = 1300 C,
◦
√
−5
−1
α = 3 · 10 K . The subsidence (7.162) can be written compactly as w(x) = w 0 x/x 0
where w 0 = 2 m,0 αT a /( m,0 − w ) and x 0 = πu/κ. Figure 7.29 shows the fitting of this
function to a data set across a ridge. The numbers above give that w 0 = 0.11 m and the
optimal value for x 0 is x 0 = 1.55 · 10 −3 m. The water depth at the ridge is 1511 m and it is
slightly more than the peak value from the observations. The depth at the ridge could have
been added as a second optimization parameter. The optimal value for x 0 gives that the
2 −1
average spreading rate is u = κx 0 /π,or u = 0.015 m/year when κ = 1·10 −6 m s .The
spreading velocity gives ∼800 km of oceanic plate at each side of the ridge after 50 Ma.