Page 253 - Physical Principles of Sedimentary Basin Analysis

7.12 Lithospheric extension and decompression melting 235

0.1 0.7 0.9
0.0 0.2 0.3 0.4 0.5 0.6 0.8 1.0
0 1.0
0.9
25
0.8
0.7
50 0.6
depth [km] 75 liquidus melt fraction [−] 0.5

100 0.4
0.3
solidus
0.2
125
0.1
150 0.0
1000 1200 1400 1600 1800 2000 −0.5 −0.4 −0.3 −0.2 −0.1 −0.0 0.1 0.2 0.3 0.4 0.5
temperature [°C] dimensionless temperature [−]
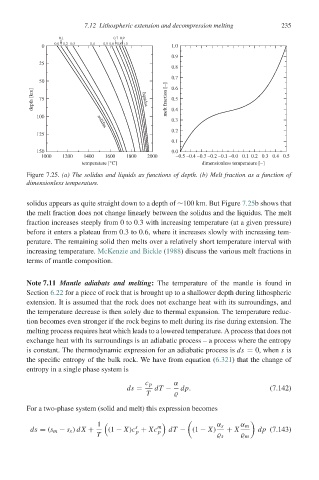
Figure 7.25. (a) The solidus and liquids as functions of depth. (b) Melt fraction as a function of
dimensionless temperature.

solidus appears as quite straight down to a depth of ∼100 km. But Figure 7.25b shows that
the melt fraction does not change linearly between the solidus and the liquidus. The melt
fraction increases steeply from 0 to 0.3 with increasing temperature (at a given pressure)
before it enters a plateau from 0.3to0.6, where it increases slowly with increasing tem-
perature. The remaining solid then melts over a relatively short temperature interval with
increasing temperature. McKenzie and Bickle (1988) discuss the various melt fractions in
terms of mantle composition.

Note 7.11 Mantle adiabats and melting: The temperature of the mantle is found in
Section 6.22 for a piece of rock that is brought up to a shallower depth during lithospheric
extension. It is assumed that the rock does not exchange heat with its surroundings, and
the temperature decrease is then solely due to thermal expansion. The temperature reduc-
tion becomes even stronger if the rock begins to melt during its rise during extension. The
melting process requires heat which leads to a lowered temperature. A process that does not
exchange heat with its surroundings is an adiabatic process – a process where the entropy
is constant. The thermodynamic expression for an adiabatic process is ds = 0, when s is
the specific entropy of the bulk rock. We have from equation (6.321) that the change of
entropy in a single phase system is

c p α
ds = dT − dp. (7.142)
T
For a two-phase system (solid and melt) this expression becomes

1
s m α s α m
ds = (s m − s s ) dX + (1 − X)c + Xc p dT − (1 − X) + X dp (7.143)
p
T s m