Page 248 - Physical Principles of Sedimentary Basin Analysis

230 Subsidence

1000 2000

800
1500
subsidence [m] 600 subsidence [m] 1000

400

500
200

0 0
0.0 0.2 0.4 0.6 0.8 1.0 0 10 20 30 40 50
3
heat production [μW/m ] crust thickness [km]
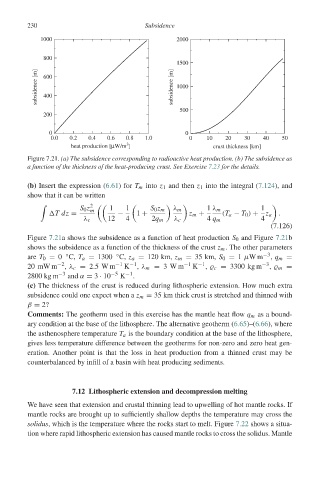
Figure 7.21. (a) The subsidence corresponding to radioactive heat production. (b) The subsidence as
a function of the thickness of the heat-producing crust. See Exercise 7.23 for the details.

(b) Insert the expression (6.61)for T m into z 1 and then z 1 into the integral (7.124), and
show that it can be written
2
S 0 z m 1 1 S 0 z m λ m 1 λ m 1
Tdz = − 1 + z m + (T a − T 0 ) + z a .
λ c 12 4 2q m λ c 4 q m 4
(7.126)
Figure 7.21a shows the subsidence as a function of heat production S 0 and Figure 7.21b
shows the subsidence as a function of the thickness of the crust z m . The other parameters
◦
◦
are T 0 = 0 C, T a = 1300 C, z a = 120 km, z m = 35 km, S 0 = 1 μWm −3 , q m =
20 mW m −2 , λ c = 2.5W m −1 K −1 , λ m = 3W m −1 K −1 , c = 3300 kg m −3 , m =
2800 kg m −3 and α = 3 · 10 −5 K −1 .
(c) The thickness of the crust is reduced during lithospheric extension. How much extra
subsidence could one expect when a z m = 35 km thick crust is stretched and thinned with
β = 2?
Comments: The geotherm used in this exercise has the mantle heat flow q m as a bound-
ary condition at the base of the lithosphere. The alternative geotherm (6.65)–(6.66), where
the asthenosphere temperature T a is the boundary condition at the base of the lithosphere,
gives less temperature difference between the geotherms for non-zero and zero heat gen-
eration. Another point is that the loss in heat production from a thinned crust may be
counterbalanced by infill of a basin with heat producing sediments.

7.12 Lithospheric extension and decompression melting
We have seen that extension and crustal thinning lead to upwelling of hot mantle rocks. If
mantle rocks are brought up to sufficiently shallow depths the temperature may cross the
solidus, which is the temperature where the rocks start to melt. Figure 7.22 shows a situa-
tion where rapid lithospheric extension has caused mantle rocks to cross the solidus. Mantle