Page 244 - Physical Principles of Sedimentary Basin Analysis

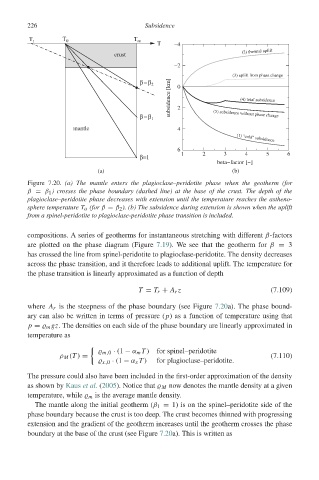
226 Subsidence

T T 0 T m
r
T −4
(2) thermal uplift
crust
−2
(3) uplift from phase change
subsidence [km] (4) total subsidence
β = β 2 0

β = β 1 2 (5) subsidence without phase change

mantle 4 (1) "cold" subsidence

6
β=1 1 2 3 4 5 6
beta−factor [−]
(a) (b)
Figure 7.20. (a) The mantle enters the plagioclase–peridotite phase when the geotherm (for
β = β 1 ) crosses the phase boundary (dashed line) at the base of the crust. The depth of the
plagioclase–peridotite phase decreases with extension until the temperature reaches the astheno-
sphere temperature T a (for β = β 2 ). (b) The subsidence during extension is shown when the uplift
from a spinel-peridotite to plagioclase-peridotite phase transition is included.

compositions. A series of geotherms for instantaneous stretching with different β-factors
are plotted on the phase diagram (Figure 7.19). We see that the geotherm for β = 3
has crossed the line from spinel-peridotite to plagioclase-peridotite. The density decreases
across the phase transition, and it therefore leads to additional uplift. The temperature for
the phase transition is linearly approximated as a function of depth

T = T r + A r z (7.109)

where A r is the steepness of the phase boundary (see Figure 7.20a). The phase bound-
ary can also be written in terms of pressure (p) as a function of temperature using that
p = m gz. The densities on each side of the phase boundary are linearly approximated in
temperature as

m,0 · (1 − α m T ) for spinel–peridotite
ρ M (T ) = (7.110)
x,0 · (1 − α x T ) for plagioclase–peridotite.
The pressure could also have been included in the first-order approximation of the density
as shown by Kaus et al. (2005). Notice that M now denotes the mantle density at a given
temperature, while m is the average mantle density.
The mantle along the initial geotherm (β 1 = 1) is on the spinel–peridotite side of the
phase boundary because the crust is too deep. The crust becomes thinned with progressing
extension and the gradient of the geotherm increases until the geotherm crosses the phase
boundary at the base of the crust (see Figure 7.20a). This is written as