Page 328 - Physical Principles of Sedimentary Basin Analysis

310 Flexure of the lithosphere

5

surface load

0
w [km]

−5
t = 0
t = 1 t e
t = 100 t
e
−10
0 200 400 600 800 1000
x [km]
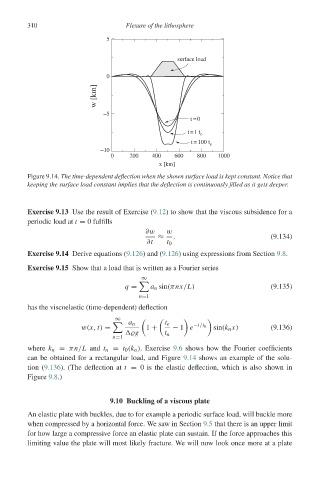
Figure 9.14. The time-dependent deflection when the shown surface load is kept constant. Notice that
keeping the surface load constant implies that the deflection is continuously filled as it gets deeper.

Exercise 9.13 Use the result of Exercise (9.12) to show that the viscous subsidence for a
periodic load at t = 0 fulfills
∂w w
≈ . (9.134)
∂t t 0
Exercise 9.14 Derive equations (9.126) and (9.126) using expressions from Section 9.8.
Exercise 9.15 Show that a load that is written as a Fourier series
∞

q = a n sin(πnx/L) (9.135)
n=1
has the viscoelastic (time-dependent) deflection
∞
a n t e
w(x, t) = 1 + − 1 e −t/t n sin(k n x) (9.136)
g t n
n=1
where k n = πn/L and t n = t 0 (k n ).Exercise 9.6 shows how the Fourier coefficients
can be obtained for a rectangular load, and Figure 9.14 shows an example of the solu-
tion (9.136). (The deflection at t = 0 is the elastic deflection, which is also shown in
Figure 9.8.)

9.10 Buckling of a viscous plate
An elastic plate with buckles, due to for example a periodic surface load, will buckle more
when compressed by a horizontal force. We saw in Section 9.5 that there is an upper limit
for how large a compressive force an elastic plate can sustain. If the force approaches this
limiting value the plate will most likely fracture. We will now look once more at a plate