Page 331 - Physical Principles of Sedimentary Basin Analysis

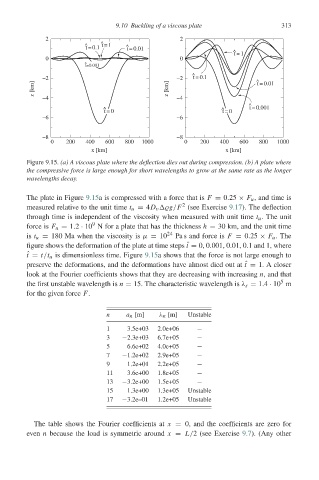
9.10 Buckling of a viscous plate 313

2 2
^
^ t = 0.1 t = 1 ^
t = 0.01
^ t = 1
0 0
^ t=0.001
^
−2 −2 t = 0.1 ^
z [km] z [km] t = 0.01
−4 −4
^
^ t = 0 ^ t = 0 t = 0.001
−6 −6

−8 −8
0 200 400 600 800 1000 0 200 400 600 800 1000
x [km] x [km]
Figure 9.15. (a) A viscous plate where the deflection dies out during compression. (b) A plate where
the compressive force is large enough for short wavelengths to grow at the same rate as the longer
wavelengths decay.

The plate in Figure 9.15a is compressed with a force that is F = 0.25 × F u , and time is
2
measured relative to the unit time t u = 4D v g/F (see Exercise 9.17). The deflection
through time is independent of the viscosity when measured with unit time t u . The unit
9
force is F u = 1.2 · 10 N for a plate that has the thickness h = 30 km, and the unit time
is t u = 180 Ma when the viscosity is μ = 10 24 Pa s and force is F = 0.25 × F u .The
figure shows the deformation of the plate at time steps ˆ t = 0, 0.001, 0.01, 0.1 and 1, where
ˆ t = t/t u is dimensionless time. Figure 9.15a shows that the force is not large enough to
preserve the deformations, and the deformations have almost died out at ˆ t = 1. A closer
look at the Fourier coefficients shows that they are decreasing with increasing n, and that
5
the first unstable wavelength is n = 15. The characteristic wavelength is λ s = 1.4 · 10 m
for the given force F.

n a n [m] λ n [m] Unstable
1 3.5e+03 2.0e+06 −
3 −2.3e+03 6.7e+05 −
5 6.6e+02 4.0e+05 −
7 −1.2e+02 2.9e+05 −
9 1.2e+01 2.2e+05 −
11 3.6e+00 1.8e+05 −
13 −3.2e+00 1.5e+05 −
15 1.3e+00 1.3e+05 Unstable
17 −3.2e–01 1.2e+05 Unstable

The table shows the Fourier coefficients at x = 0, and the coefficients are zero for
even n because the load is symmetric around x = L/2 (see Exercise 9.7). (Any other