Page 335 - Physical Principles of Sedimentary Basin Analysis

10.1 Newton’s law of gravity 317

68
−2200
−2000 −200
−1800
−1400 −1600
latitude [deg] 67 −1200 −400 [m] 0

−1000

−800 −500
−1000
−1500
−2000
−600 −2500
66
6 7 8 9 10 11
longitude [deg]
(a)
68
70
50
40
latitude [deg] 67 −20 −10 −30 90 80 [mGal]

100
80
60
60 40
30 10 20
0
−20
20 0 −40
66
6 7 8 9 10 11
longitude [deg]
(b)
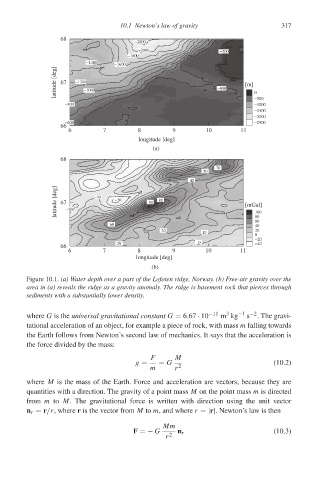
Figure 10.1. (a) Water depth over a part of the Lofoten ridge, Norway. (b) Free-air gravity over the
area in (a) reveals the ridge as a gravity anomaly. The ridge is basement rock that pierces through
sediments with a substantially lower density.

3
s
where G is the universal gravitational constant G = 6.67 · 10 −11 m kg −1 −2 . The gravi-
tational acceleration of an object, for example a piece of rock, with mass m falling towards
the Earth follows from Newton’s second law of mechanics. It says that the acceleration is
the force divided by the mass:
F M
g = = G (10.2)
m r 2

where M is the mass of the Earth. Force and acceleration are vectors, because they are
quantities with a direction. The gravity of a point mass M on the point mass m is directed
from m to M. The gravitational force is written with direction using the unit vector
n r = r/r, where r is the vector from M to m, and where r =|r|. Newton’s law is then

Mm
F =− G n r (10.3)
r 2