Page 332 - Physical Principles of Sedimentary Basin Analysis

314 Flexure of the lithosphere

10

F = 0.25F u
5

log 10 (t 0 ) [Ma] 0 F = 2.5F u

−5

−10
3 4 5 6 7 8
log (λ) [m]
10
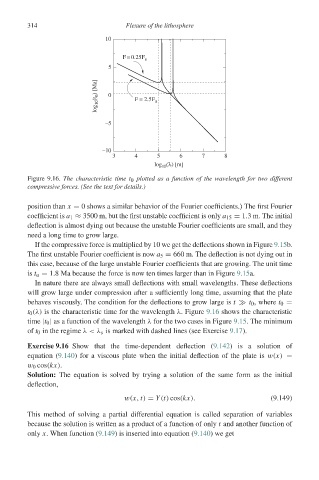
Figure 9.16. The characteristic time t 0 plotted as a function of the wavelength for two different
compressive forces. (See the text for details.)

position than x = 0 shows a similar behavior of the Fourier coefficients.) The first Fourier
coefficient is a 1 ≈ 3500 m, but the first unstable coefficient is only a 15 = 1.3 m. The initial
deflection is almost dying out because the unstable Fourier coefficients are small, and they
need a long time to grow large.
If the compressive force is multiplied by 10 we get the deflections shown in Figure 9.15b.
The first unstable Fourier coefficient is now a 5 = 660 m. The deflection is not dying out in
this case, because of the large unstable Fourier coefficients that are growing. The unit time
is t u = 1.8 Ma because the force is now ten times larger than in Figure 9.15a.
In nature there are always small deflections with small wavelengths. These deflections
will grow large under compression after a sufficiently long time, assuming that the plate
behaves viscously. The condition for the deflections to grow large is t
t 0 , where t 0 =
t 0 (λ) is the characteristic time for the wavelength λ. Figure 9.16 shows the characteristic
time |t 0 | as a function of the wavelength λ for the two cases in Figure 9.15. The minimum
of t 0 in the regime λ<λ s is marked with dashed lines (see Exercise 9.17).
Exercise 9.16 Show that the time-dependent deflection (9.142) is a solution of
equation (9.140) for a viscous plate when the initial deflection of the plate is w(x) =
w 0 cos(kx).
Solution: The equation is solved by trying a solution of the same form as the initial
deflection,
w(x, t) = Y(t) cos(kx). (9.149)

This method of solving a partial differential equation is called separation of variables
because the solution is written as a product of a function of only t and another function of
only x. When function (9.149) is inserted into equation (9.140) we get